Вероятность попадания случайной величины в заданный интервал
Может быть вычислена двумя способами:
1) через функцию распределения 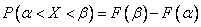
2) через плотность распределения 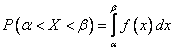
Математическое ожидание случайной величины
1) Для дискретной случайной величины  , заданной рядом распределения:
, заданной рядом распределения:
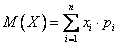
1) Для непрерывной случайной величины  , заданной плотностью распределения :
, заданной плотностью распределения :
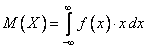 .
.
Дисперсия случайной величины
По определению дисперсия – это второй центральный момент: 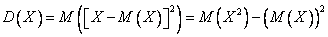 .
.
1) Для дискретной случайной величины  , заданной рядом распределения:
, заданной рядом распределения:
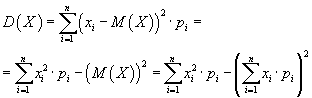
1) Для непрерывной случайной величины  , заданной плотностью распределения :
, заданной плотностью распределения :
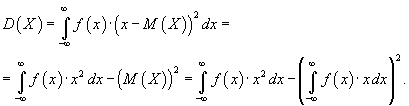
Среднее квадратическое отклонение случайной величины
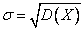
Начальный момент r–го порядка случайной величины
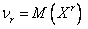 .
.
В частности, первый начальный момент – это математическое ожидание: 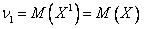
Центральный момент r – го порядка случайной величины
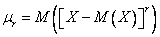
В частности, второй центральный момент – это дисперсия: 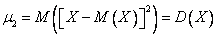 .
.
Асимметрия
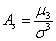
Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого (правая часть кривой более пологая), и отрицателен в противном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.
Эксцесс
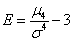
Коэффициент эксцесса нормального распределения равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик гладкий
|
|
|
III. Распределения случайных величин. Основные формулы онлайн
Спасибо, что читаете и делитесь с другими
Биномиальное распределение (дискретное)
 - количество «успехов» в последовательности из
- количество «успехов» в последовательности из 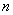 независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна
независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна  .
. 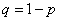 .
.
Закон распределения  имеет вид:
имеет вид:
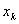
| 0 | 1 | ….. | k | ….. | 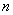
|
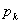
| 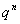
| 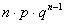
| 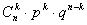
| 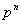
|
Здесь вероятности находятся по формуле Бернулли:  .
.
Характеристики: 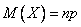 ,
, 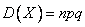 ,
, 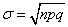
Примеры многоугольников распределения для 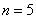 и различных вероятностей:
и различных вероятностей:
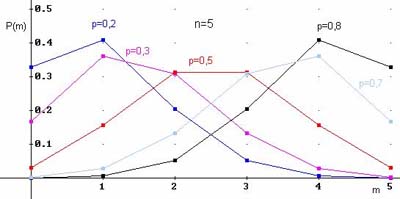
Пуассоновское распределение (дискретное)
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
При условии 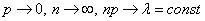 закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность
закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность  события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Ряд распределения:
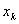
| 0 | 1 | ….. | k | ….. |
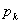
| 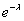
| 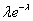
| ….. | 
| ….. |
|
|
|
Вероятности вычисляются по формуле Пуассона: 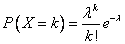 .
.
Числовые характеристики: 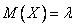 ,
, 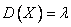 ,
, 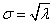
Разные многоугольники распределения при 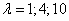 .
.
Показательное распределение (непрерывное)
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Плотность распределения:
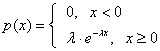
Где 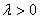 .
.
Числовые характеристики: 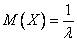 ,
, 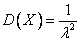 ,
, 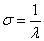
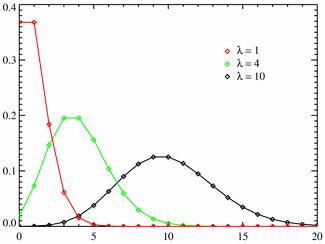
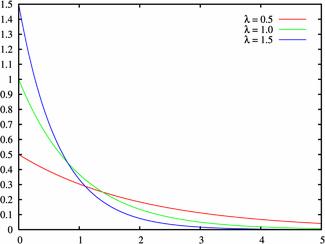
Плотность распределения при различных значениях 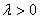 .
.
Дата добавления: 2019-03-09; просмотров: 189; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
