МЕТОД ПОСЛЕДОВАТЕЛЬНОГО ИСКЛЮЧЕНИЯ НЕИЗВЕСТНЫХ  (МЕТОД ГАУССА)

Рассмотрим еще один метод решения линейных систем, называемый методом последовательного исключения неизвестных или методом Гаусса. Этот метод в общем виде впервые предложил немецкий математик Карл Фридрих Гаусс (1777—1855).

Решая систему линейных алгебраических уравнений методом Гаусса, преобразования совершают не над уравнениями, а над матрицей из коэффициентов при неизвестных и свободных членов (расширенной матрицей системы), т.е. рассматривая матрицу

,

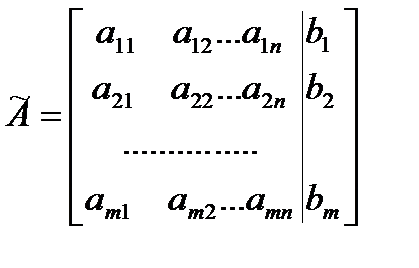где вертикальной чертой отделен столбец, составленный из свободных членов. С помощью элементарных преобразова­ний эту матрицу можно привести к одному из трех видов: «треугольной», трапециевидной или к матрице, одна строка которой состоит из нулей, кроме отличного от нуля числа в столбце для свободных членов.

Пример 1

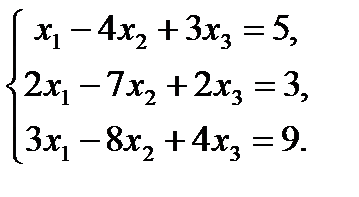
Составим расширенную матрицу системы и преобразуем её:

.

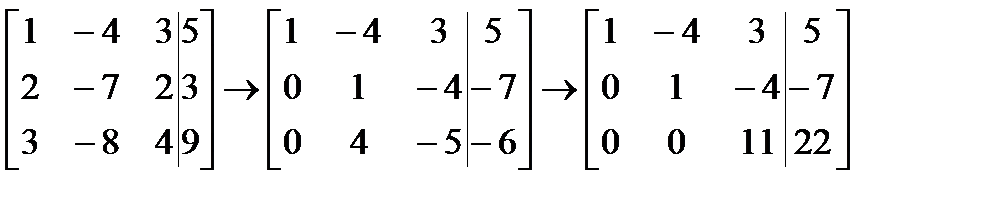Вторая матрица получена из первой в результате следующих действий:

1) вторая строка сложена с первой, умноженной на (-2);

2) третья строка сложена с первой, умноженной на (-3);

3) третья матрица получена со второй матрицы – вторая строка умножена на (-4) и прибавлена к третьей строке.

Последней матрице соответствует система уравнений

 

 

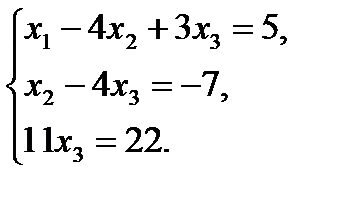
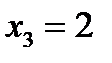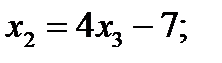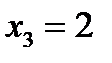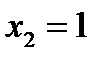Из третьего уравнения находим . Второе уравнение даёт возможность определить х₂:  так как то . Из первого уравнения находим:  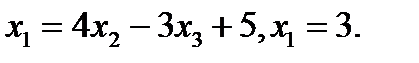Следовательно полученная система имеет решение:  Это же решение имеет и исходная система.

Пример 2

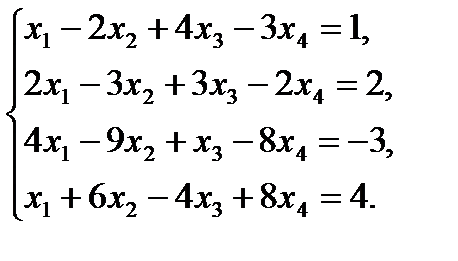
Составим расширенную матрицу системы и преобразуем её, прибавляя к первой строке вторую и четвертую, умноженные соответственно на числа (-2), (-4), -(1)

Последняя матрица получена из предыдущей путём умножения третьей строки на  и прибавления к четвёртой строке. Этой матрице соответствует система уравнений

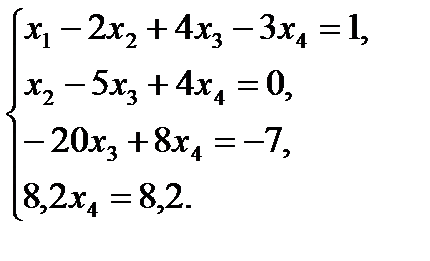
Решая эту систему, находим: , , .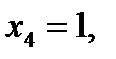

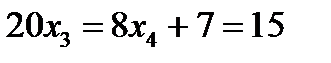
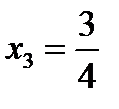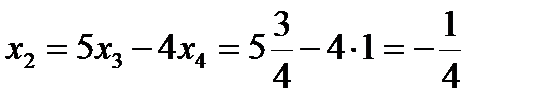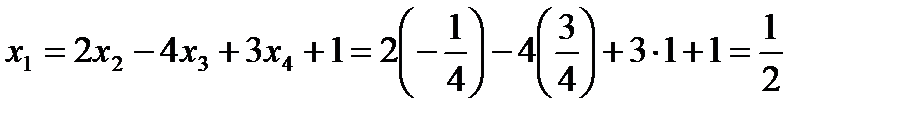Следовательно данная система имеет единственное решение

, , , .

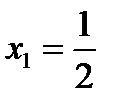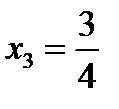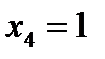Пример 3

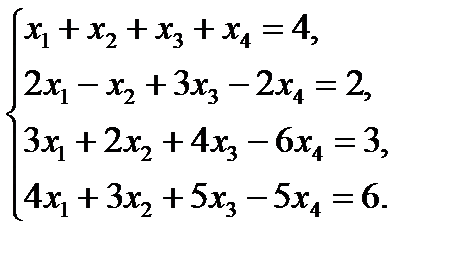
Записывая соответствующую матрицу и совершая преобразования, умножаем поочередно первую строку на (-2), (-3), (-4) и складываем со второй, третьей и четвертой строками, получаем

 

Третья матрица получена из предыдущей перестановкой последних трёх строк. Последней матрице соответствует система уравнений

 

Эта система несовместна, так как никакие значения неизвестных не могут удовлетворить её третьему уравнению.

Следовательно, исходная система также несовместна.

Замечание. Если в процессе преобразования матрицы системы получится строка, в которой равны нулю все элементы, за исключением одного, соответствующего свободному члену, то такая система несовместна.

Пример 4

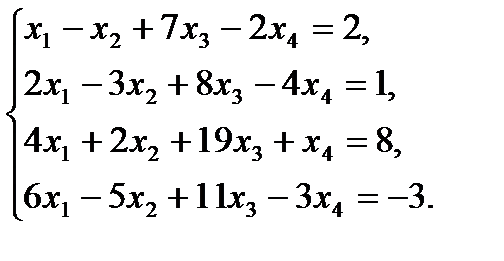
Составляем матрицу и преобразуем её:

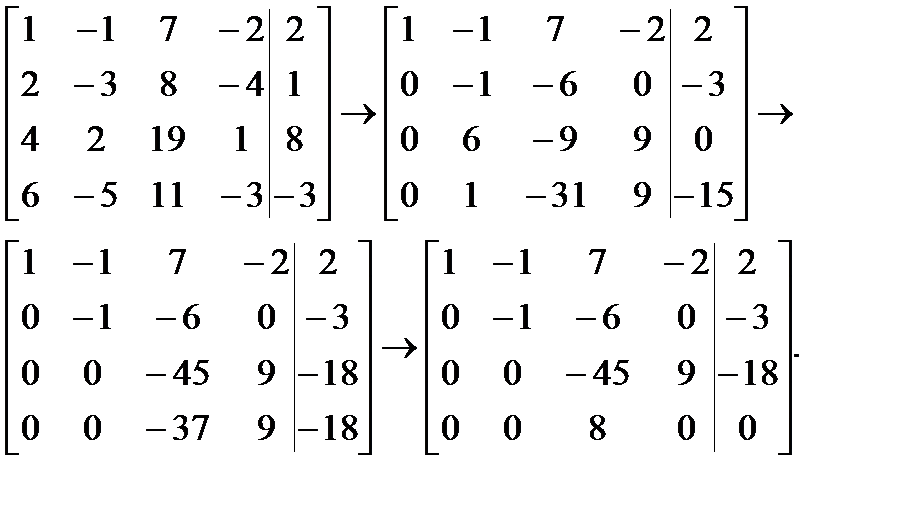
Последняя матрица получена в результате сложения четвертой строки и третьей строки, умноженной на (-1). Этой матрице соответствует система уравнений

имеющая решение: , , , .

 

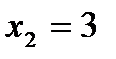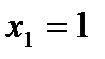Пример 5

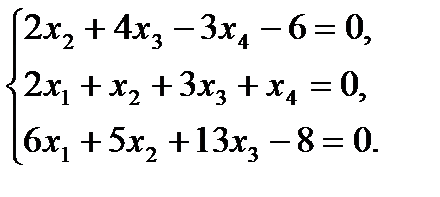
Данная система является неоднородной. Коэффициент при х₁ в первом уравнений равен нулю, т.е. а₁₁=0. Чтобы применить метод Гаусса, необходимо поменять местами, например, первое и второе уравнения и перенести свободные члены в правые части:

Это неоднородная система трёх уравнений относительно четырёх неизвестных. Составляем матрицу и преобразуем её:

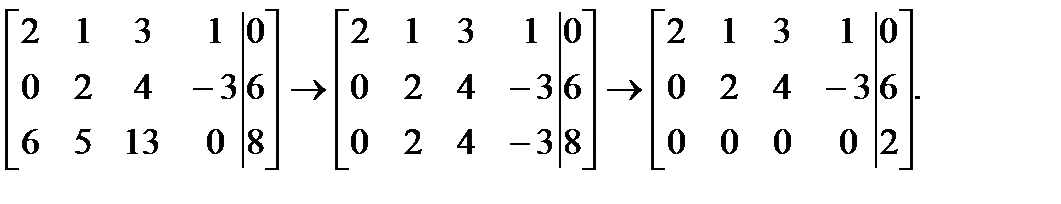
Отсюда видно, что система несовместна, так как последняя строка третьей матрицы соответствует уравнению, которому не могут удовлетворить никакие значения неизвестных.

---

Дата добавления: 2019-03-09; просмотров: 183; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!