Глава II. Энергия активации и предэкспоненциальный множитель
Химический факультет
КАФЕДРА Физической химий и химической экологии
КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ
ФИЗИЧЕСКАЯ ХИМИЯ
Уравнение Аррениуса. Вычисление энергии активации и предэкспоненциального множителя из экспериментальных данных
| Выполнил: Студент(ка) 4 курса очной формы обучения Направление подготовки 04.03.01 Химия Профиль ВМС_________________________ | |||
| Тимофеева Дарья Витальевна Проверил: к.х.н., доцент Насретдинова Р.Н. _________________ (подпись) «___»____________20____г. |
УФА – 2017
Содержание
Введение 3
Глава I.Уравнение Аррениуса 4
Глава II. Глава II. Энергия активации и предэкспоненциальный множитель 7
Глава III. Экспериментальное вычисление параметров уравнения 19
Заключение 10
Список использованной литературы 11
Введение
В лабораторном практикуме по химической кинетике часто проводят эксперименты с непременной обработкой константы скорости химической реакции. Чем же исследователи пользуются? Какими параметрами оперируют? И к каким результатам это приводит - довольно актуальные вопросы.
|
|
|
Работа разделена на три части. В первой опора сделана на уравнение Аррениуса. Показан его вывод, а именно, переход от изобары Вант-Гоффа.
Во второй на энергию активации и на предэкспонециальный множитель. Их неразрывную связь.
Некоторые ученые считают, что все методы оценки константы скорости реакции хороши, но наиболее обоснованно выражает температурную зависимость уравнение Аррениуса. Приведено экспериментальное описание кинетических процессов с помощью аналитических и графических расчетов.
Актуальность выбранной темы такова, что без определения энергии активации реакции невозможно запустить процессы, потенциально реализуемые в системе. Степень изученности темы определяется исследованиями различных технических институтов в сотрудничестве физико-химическими объединениями.
Цель работы в том, чтобы кратко и точно охарактеризовать каждую шаг вычисления. А задачами являются разбиение комплексной темы на элементарные области. В конце работы дана литература для уточнения информации. Помимо основных источников есть и дополнительные, знакомство с которыми должно способствовать многофункциональному пониманию темы. Каждому хорошему химику нужно уметь пользоваться справочниками, оперировать параметрами, чтобы в заключении свести все теоретические выводы к единому и практическому целому.
|
|
|
Глава I . Уравнение Аррениуса
В 1889 г. шведский ученый Сванте Аррениус на основании экспериментов вывел уравнение, которое названо его именем:
,
где k – константа скорости реакции; А – предэкспоненциальный множитель; е – основание натурального логарифма; Еа – постоянная, называемая энергией активации, определяемая природой реакции. Значения Еа для химических реакций лежат в пределах 40 – 400 кДж/ моль.
После логарифмирования уравнение имеет вид
| (рис 1) |
Здесь tgα = -Еа/R и Еа = - Rtgα. Отрезок, отсекаемый на оси ординат равен lnА.
Итак, константа скорости реакции (и скорость) возрастает с увеличением температуры по экспоненциальному закону. В соответствии с уравнением Аррениуса константа скорости реакции уменьшается с ростом энергии активации. Уравнение Аррениуса позволяет рассчитывать константы скорости (и скорости) при различных температурах.
|
|
|
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):
Рис. 2.6 Распределение частиц по энергии
Здесь nЕ/N – доля частиц, обладающих энергией E;
Ei - средняя энергия частиц при температуре Ti (T1 < T2 < T3)
Рассмотрим термодинамический вывод выражения, описывающего зависимость константы скорости реакции от температуры и величины энергии активации – уравнения Аррениуса. Согласно уравнению изобары Вант-Гоффа,
(II.31)
Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:
(II.32)
Представив изменение энтальпии реакции ΔHº в виде разности двух величин E1 и E2, получаем:
(II.33)
(II.34)
Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где EA – энергия активации:
|
|
|
(II.35)
После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:
(II.36)
А экспоненцированием получаем само уравнение Аррениуса:
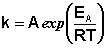(II.37)
Глава II. Энергия активации и предэкспоненциальный множитель
Аррениус также предположил, что реагировать между собой могут только те молекулы, которые находятся в активной форме, образующиеся из обычных молекул. Такие молекулы были названы активными, а энергия, необходимая для перевода обычных молекул в активное состояние, энергией активации.
В самом деле, в ходе химической реакции разрушаются одни и возникают другие молекулы, происходит изменение химических связей, т.е. перераспределение электронной плотности. Если бы старые связи в ходе реакции сразу полностью разрушались, то на это потребовалось бы большое количество энергии, и реакция протекала крайне медленно. Как показали исследования, в ходе реакции система проходит через переходное состояние, через образование активированного комплекса. Например, ход реакции
АВ + DC = AD + BC
В активированном комплексе старые связи еще не разорваны, но уже ослаблены, новые связи наметились, но еще не образовались. Время существования его не велико (10‾14 – 10‾11 с). При распаде комплекса образуются либо продукты реакции, либо исходные вещества. Для образования переходного комплекса необходима энергия. Система в переходном состоянии имеет более высокую энергию, чем в исходном и конечном состояниях.
Энергия, необходимая для перехода вещества в состояние активированного комплекса, называется энергией активации.
Образование активированного комплекса определяется энергией молекул. Молекула, энергия которой достаточна для образования активированного комплекса, называется активной. Доля таких молекул зависит от температуры. При высоких температурах доля активных молекул, энергия которых равна или выше энергии активации, велика и, соответственно, растет доля молекул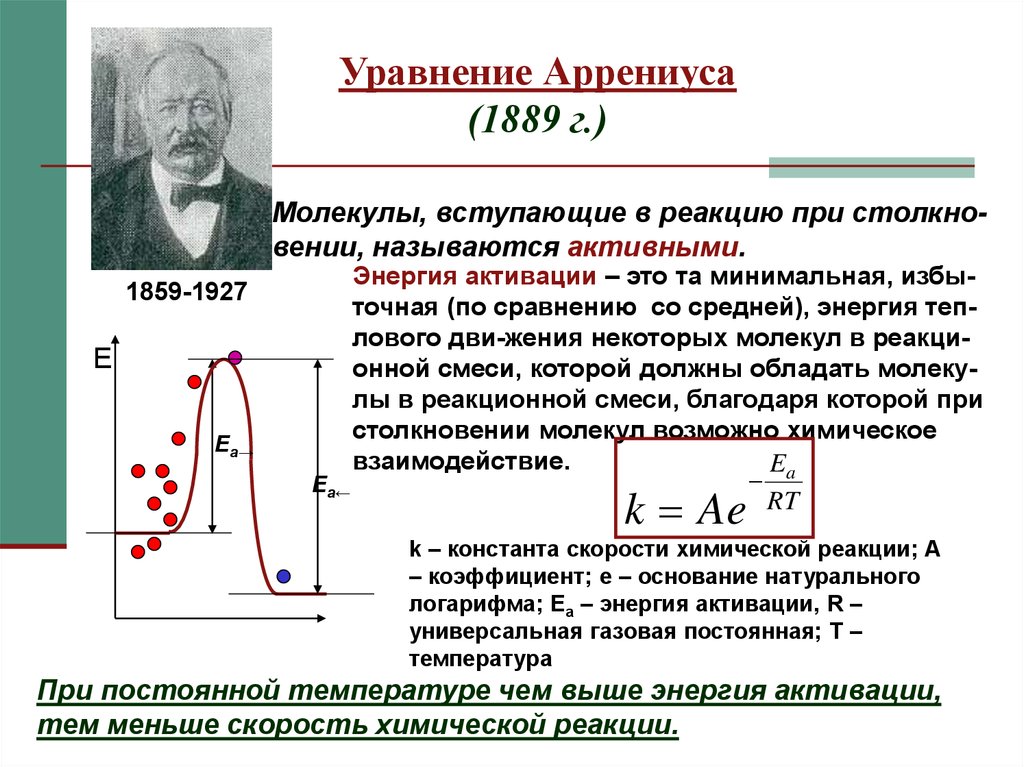 
способных к активным столкновениям с образованием активированного комплекса, т.е. реакции идут быстро. Чем выше энергия активации, тем меньше доля частиц, способных к активному взаимодействию. Экзотермические реакции протекают с меньшей энергией активации, чем эндотермические (рис.18). Высокая энергия активации (высокий энергетический барьер) является причиной того, что многие химические реакции при невысоких температурах не протекают, хотя термодинамически возможны (ΔG <0).
Итак, энергия активации – это энергия, необходимая для перехода частиц в состояние активированного комплекса. Частицы, энергия которых равна или выше энергии активации, называются активными. С ростом температуры растет доля этих частиц и соответственно скорость реакции. С увеличением энергии активации уменьшается доля активных молекул и скорость реакции. Следовательно, предэкспоненциальный множитель - это то число столкновений реагирующих молекул в единицу времени в единице объема при их концентрациях, равных одному молю. В случае, если температура начнет стремится к бесконечности, множитель будет равняться максимальному значению константы скорости химической реакции.
Дата добавления: 2019-02-26; просмотров: 3025; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!