Общие теоретические положения
Первоначально, исходя из условия задачи, надо определить входной алфавит, т.е. символы, которые будут находиться на ленте для данной задачи. В процессе решения задачи – написания алгоритма для работы МТ входной алфавит может быть дополнен.
Затем придумать идею алгоритма, т.е. как будет двигаться головка МТ – управляющая головка (УГ), где будет начальное ее положение. Алгоритм работы МТ может немного напоминать алгоритм сортировки (надеюсь, что не запутала вас). Начальное положение головки МТ вы выбираете сами, исходя из идеи алгоритма. Так как лента бесконечная, то для конкретной задачи, для упрощения ее решения можно ограничить последовательность символов некоторыми специальными, либо ввести в рассмотрение знак пробела.
Определить начальное состояние. В большинстве случаев, это первое из состояний, записанных в таблице.
Получается, что в соответствии с алгоритмом УГ бегает направо – налево вдоль ленты и производит предписанные алгоритмом действия.
Для упрощения построения алгоритма можно нарисовать частный случай задачи и на нем попытаться придумать алгоритм, а потом, когда станет ясна идея, переделать алгоритм для любого варианта расположения символов на ленте для данной задачи.
Задача 1.
Построить МТ, которая определяет четность или нечетность числа 1 в строке. Конец последовательности помечается символом В, затем в эту ячейку будет записан результат.
|
|
|
Допущение: Управляющая головка (УГ) находится под первым символом последовательности (если специально не оговорено, определяется человеком решающим задачу).
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | В | |||||
| ^ |
Алгоритмическая идея: МТ требуется 2 состояния: одно для нечетного числа 1, другое для четного. Исходя из условия, результат будет записан в ячейку с символом В – 0 при четном числе 1, 1 – при нечетном. Для учета уже посчитанных/пройденных 1, каждая встретившаяся и учтенная 1 стирается, т.е. на ее место записывается 0.
| S1 | S2 | Установим: S1 – состояние для четного числа 1, S2 – для нечетного. | |
| 0 | S1 П | S2 П | В начальный момент времени, находимся в состоянии S1 |
| 1 | 0 S2 П | 0 S1 П | |
| B | 0 S1 ! | 1 S2 ! |
Действие: УГ устанавливается в очередную ячейку. Если там записана 1, то на ее место записывается 0, МТ переходит в противоположное состояние, и УГ передвигается в следующую ячейку. Движение УГ слева направо. Если в рассматриваемой ячейке записан 0, то состояние не меняется, УГ передвигается вправо к следующей ячейке. Если встретился символ В – надо анализировать, в каком состоянии находится МТ в этот момент. Если в S1, то на место В записывается 0, если в S2, то записывается 1 и происходит остановка МТ.
|
|
|
Задача 2.
Построить МТ, для проверки скобочных выражений. МТ должна решить, является ли последовательность из левых и правых скобок правильной, т.е. каждой левой скобке ( должна соответствовать правая ). Начало и конец последовательности ограничены символами А.
Допущение: Управляющая головка (УГ) находится под первой слева скобкой.
| 0 | 0 | А | ( | ( | ) | ( | ) | ) | А | |||
| ^ |
Алгоритмическая идея: Ищется первая правая ) скобка, затем первая левая (, ей парная, и обе заменяются символом Х. Вычеркивание парных скобок продолжается до тех пор, пока не произойдет одно из событий:
1) МТ, продвигаясь влево не находит парного символа ( , при достижении символа А она на его месте печатает символ 0 и останавливается.
2) МТ, продвигаясь вправо не находит ни одного символа ) и достигает символа А. В этом случае МТ начинает движение влево и проверяет – не остался ли какой-то из символов ( :
· Если такой ( символ найден, то на месте А печатается 0
|
|
|
· Если нет символа ( , то на месте символа А печатается 1.
Состояние S1 предписывает движение вправо (П)
Состояние S2 предписывает движение влево (Л)
Состояние S3 предписывает движение влево (Л), когда не найдено ни одной ")". Т.е. головка приходит к правому А и при продвижении влево при нахождении "(" переходит в S4, для того, чтобы поставить символ 0 вместо левого А
Начальное состояние S1.
| S 1 | S 2 | S 3 | S 4 | |
| ) | Х S2 Л | Л | - | - |
| ( | П | Х S1 П | S4 Л | Л |
| А | S3 Л | 0 ! | 1 ! | 0 ! |
| Х | П | Л | Л | Л |
Прочерк "-" в программе МТ означает, что быть такой ситуации для данной задачи не может.
Задача 3. Построить МТ, переворачивающую любое слово в алфавите А={а,в}. Т.е. построить зеркальное отображение заданного слова.
Например.
Чтобы знать, где начинается слово, в соответствующую ячейку ленты запишем *. Конец последовательности символов слова означает пробел (Æ).
| * | а | а | в | а | в | Æ | Æ | Æ | ||||
| ^ |
Таким образом, алфавит для написания программы МТ будет состоять из: а, в, *, Æ.
Алгоритмическая идея: УГ устанавливается на последний символ слова. МТ находится в состоянии S1. Если это символ алфавита А={а,в}, то символ стирается, т.е. вместо него ставиться пробел Æ, МТ переходит в другое состояние, УГ начинает движение направо и ищет первый пробел. Найдя его она печатает на его месте стертый символ и переходит в состояние, отвечающее за продвижение налево, т.е. за возврат к анализируемому слову. В этом состоянии УГ движется налево до первого пробела, а найдя его сдвигается еще раз налево (к следующей ячейке) и переходит в состояние S1, отвечающее нахождение очередного символа слова для стирания. Если в состоянии S1 МТ в ячейке обнаруживает *, то это означает, что все символы проанализированы, зеркальное отображение построено. Происходит останов МТ.
|
|
|
Пошаговый пример построения зеркального отображения слова.
| * | а | а | в | а | в | Æ | Æ | Æ | ||||
| ^ |
| * | а | а | в | а | Æ | в | Æ | Æ | ||||
| ^ |
| * | а | а | в | а | Æ | в | Æ | Æ | ||||
| ^ ® |
| * | а | а | в | Æ | Æ | в | а | Æ | ||||
| ^ |
| * | а | а | в | Æ | Æ | в | а | Æ | ||||
| ^ |
| * | а | а | Æ | Æ | Æ | в | а | в | Æ | Æ | ||
| ^ |
| * | а | а | Æ | Æ | Æ | в | а | в | Æ | Æ | ||
| ^ |
| * | а | Æ | Æ | Æ | Æ | в | а | в | а | Æ | ||
| ^ |
| * | а | Æ | Æ | Æ | Æ | в | а | в | а | Æ | ||
| ^ |
| * | Æ | Æ | Æ | Æ | Æ | в | а | в | а | а | ||
| ^ |
| * | Æ | Æ | Æ | Æ | Æ | в | а | в | а | а | ||
| ^ |
Программа МТ
Начальное состояние S1.
| S 1 | S 2 | S 3 | S 4 | |
| а | Æ S2 П | П | П | Л |
| в | Æ S3 П | П | П | Л |
| * | ! | - | - | - |
| Æ | Л | а S4 Л | в S4 Л | S1 Л |
Состояния S2 и S3 отличаются тем, что на месте найденного пробела в одном случае (S2) печатают "а", соответственно вместо стертой "а", а в другом печатается "в".
Задача 4. Построить МТ для сложения двух чисел в унарной с/с.
Например.
| | | | | | | + | | | | | | | ||||||
| ^ |
Алгоритмическая идея. Перенести все символы второго числа на свободное место перед первым числом, таким образом, все символы окажутся вместе – получится суммарное унарное число.
УГ установить на последний символ второго числа. Записать на его место пробел (стереть символ), перейти в другое состояние (чтобы при встрече очередной "|" выполнять другие действия, а не стирания, как в предыдущем состоянии) и двигаться налево до первого пробела. Найдя его, записать на его место стертую "|" и перейти в другое состояние, отвечающее за движение направо – для поиска очередного символа второго числа. Действовать, пока все "|" второго числа не будут записаны перед первым числом.
Программа МТ
Начальное состояние S1.
| S 1 | S 2 | S 3 | |
| 1 | Æ S2 Л | Л | П |
| Æ | - | 1 S3 Л | S1 Л |
| + | ! | Л | П |
Есть еще вариант. Последний символ второго унарного числа перенести на место "+". Получится суммарное унарное число ни чем не разделенное.
Но в этом случае надо быть точно уверенным, что между числами и знаком "+" не стоят никакие другие символы (пробелы и т.п.), либо проверять.
Нормальный алгоритм Маркова
К исходному слову P применяют по порядку каждую пару из схемы подстановок. Если подстановка возможна, то ее осуществляют и все начинают сначала. Выполнение алгоритма прекращается, когда нет ни одной допустимой подстановки. В результате получается конечное слово Q.
Например, нормальная схема: ab ->ba, ac -> ab, aa -> bc.
Если входное слово acabba, то:
acabba -> acbaba -> acbbaa -> abbbaa -> babbaa -> bbabaa -> bbbaaa -> bbbbca.
То, что ниже взяла из инета, но вроде тоже читаемо.
Основная операция при работе алгоритмов Маркова – это переработка слов в некотором алфавите. Эта переработка заключается в производстве некоторого количества замен определенных последовательностей символов. Эти замены совершаются в СТРОГО определенном порядке, а именно: после каждой замены алгоритм читается с самого начала, а слово анализируется с самого первого символа. В отличие от машин Тьюринга, алгоритмы Маркова выполняются без какого – либо устройства, осуществляющего движения и имеющего внутреннюю память. В данном случае мы можем оперировать только ленточными знаками. Сама лента в этом случае не разделяется на строгие ячейки, а имеет гибкую основу, что позволяет ей растягиваться и сжиматься исходя из того, увеличивается ли в слове число символов или уменьшается.
Формат команды (строки) следующий
{ai} à {bj} [•],
где
{ai} – последовательность символов, которая ищется в слове
à - знак перехода к операции записи
{bj} - последовательность символов, которая записывается вместо найденной
[•] - знак принудительного окончания алгоритма (необязательный параметр)
Программа (алгоритм) представляет собой совокупность строк указанного вида, причем порядок строк имеет важнейшее значение. Окончание работы алгоритма происходит в тот момент, когда выполняется строка, содержащая знак принудительной остановки, либо тогда, когда более ни одна строка не может быть выполнена (в слове нет ни одной из искомых последовательностей символов).
Например, алгоритм, состоящий из одной строки, вида
0 à *
будучи примененным к слову в алфавите {0,1}, заменит все нули на звездочки.
В свою очередь алгоритм
0 à * •
будучи примененным к слову в алфавите {0,1}, заменит на звездочку первый встреченный ноль.
Довольно сложная для реализации на машинах Тьюринга задача сортировки слова по возрастанию, допустим в алфавите {0,1,2}, решается при помощи Маркова весьма изящно:
20 à 02
10 à 01
21 à 12
Некоторые задачи переработки слов нельзя решить без расширения алфавита.
Например, дано произвольное двоичное слово. Надо убрать из него два первых знака.
Рассмотрим алгоритм вида:
00 à •
01 à •
10 à •
11 à •
Если в слове случайно первыми двумя символами были нули (например, «001011»), то алгоритм действительно выполнит указанную задачу. Также работа закончится успешно, если в слове ни разу не встретилось два нуля подряд, а первыми символами оказалась пара 01 (например, «01011101»). Но в слове 1100101 выбросятся два нуля, которые вовсе не являются первыми символами слова. В этом случае существующий алфавит надо расширить вспомогательными буквами, которых нет в начальном слове и которые появляются в ходе вычисления. По сути, это некоторые аналоги внутренней памяти (состояний машин Тьюринга). Они вводятся с помощью формулы λ à α (α – вспомогательная буква) или, что более корректно, пары формул
λ 0 à α 0
λ 1 à α 1
Применив такие продукции к слову λ 1100101 λ получим:
λ α 1100101 λ
Дальше мы «тащим» эту букву по слову вправо, стирая и отсчитывая символы
(стерли первый):
α 0 à β
α 1 à β
(стерли второй):
β 0 à •
β 1 à •
Однако если мы расположит эти строки в обычном порядке, а именно:
λ 0 à α 0
λ 1 à α 1
α 0 à β
α 1 à β
β 0 à •
β 1 à •
алгоритм будет работать совсем не так, как хотелось бы. В частности вся его деятельность будет сводиться к созданию бесконечно большого числа символов α поочередно со стиранием символов слова. Это связано с тем, что после выполнения каждой замены управление передается снова первой строке, а слово анализируется с левого символа. Поэтому чаще всего алгоритм пишется как бы «снизу-вверх», т.е. в самом начале ставятся строки, относящиеся к группе «окончание алгоритма», далее «тело программы» и в самом низу блок «инициализация», которая будет выполняться только однажды, а затем управление перейдет к более ранним строкам.
Правильный алгоритм выглядит следующим образом.
β 0 à •
β 1 à •
α 0 à β
α 1 à β
λ 0 à α 0
λ 1 à α 1
Ту же самую задачу можно решить и использовав всего один дополнительный символ:
α00 à•
α01 à•
α10 à•
α11 à•
α0 à•
α1 à•
λ 0 à α 0
λ 1 à α 1
Задание к работе:
Элементарные машины — это машины с алфавитом {s0, |}, получаемым присоединением к однобуквенному алфавиту {|} пустой буквы s0. Результатом их применения к записи на ленте являются некоторые элементарные изменения (преобразования) этой записи.
Пример 1.
Машина А, имеющая программу, данную в таблице 5, выше уже рассмотрена.
Таблица 5
| A | s0 | | |
| q1 | |Нq0 | |Пq1 |
Пример 2.
Машина B воспринимает любое число из набора x1, x2, ..., xn, уменьшает число палочек в его записи на одну и останавливается, воспринимая уменьшенное число. Так работает машина с программой, данной в таблице 6.
Таблица 6
| B | s0 | | |
| q1 | s0Лq0 |
Задача 2.
Изобразите на ленте в алфавите {s0, |} набор чисел 2, 3, 4 и пусть машина В воспринимает второе число в стандартном положении. Изобразите ленту после работы машины. Какой набор чисел будет записан на ней?
Пример 3.
Машина C воспринимает набор чисел x1, x2, ..., xn в стандартном положении и через одну пустую ячейку справа от этого набора записывает число 0, после чего останавливается, воспринимая 0.
Программа машины C представлена таблицей 7.
Таблица 7
| C | s0 | | |
| q1 | s0Пq2 | |Пq1 |
| q2 | |Нq0 |
Пустая клетка таблицы означает, что пара (|, q2) не возникает в процессе работы этой машины (поэтому можно записать в этой клетке произвольную команду).
Задача 3.
Изобразите на ленте в алфавите {s0, |} набор чисел 1, 2, 3 и имитируйте работу машины C (изобразите ленту после каждого такта машины до ее остановки).
Пример 4.
Машина D, отправляясь от воспринятого в стандартном положении числа, не самого правого на ленте, заполняет промежуток из пустых клеток (если имеется такой) между этим числом и ближайшим справа, оставляя между ними пустую клетку, и останавливается, воспринимая в стандартном положении получающееся число.
Так, машина D, примененная к ленте
| s0 | | | | | s0 | s0 | s0 | | | s0 | | | | | s0 | s0 | s0 | ||
| q1 |
в качестве результата выдает следующую запись на ленте:
| s0 | | | | | | | | | s0 | | | s0 | | | | | s0 | s0 | s0 | ||
| q0 |
Так работает машина с программой, данной в таблице 8.
Таблица 8
| D | s0 | | |
| q1 | |Пq2 | |
| q2 | |Пq2 | |Лq3 |
| q3 | s0Лq0 |
Задача 4.
Изобразите на ленте числа 3 и 2 в алфавите {s0, |}, отделенные друг от друга четырьмя пустыми ячейками. Имитируйте работу машины D применительно к этой записи на ленте.
Пример 5.
Машина r, примененная к произвольной записи на ленте, сдвигает воспринимаемую ячейку на одну ячейку вправо и затем останавливается, не изменяя записи на ленте.
Так работает машина с программой, данной в таблице 9.
Таблица 9
| r | s0 | | |
| q1 | s0Пq0 | |Пq0 |
Пример 6.
Машина l, примененная к произвольной записи на ленте, сдвигает воспринимаемую ячейку на одну ячейку влево и затем останавливается, не изменяя записи на ленте.
Задача 5.
Составьте программу машины l.
| l | s0 | | |
| q1 | s0Лq0 | |Лq0 |
Пример 7.
Машина R, отправляясь от воспринятого в стандартном положении числа, не самого правого на ленте, идет вправо к стандартному положению ближайшего справа числа.
Программа машины R помещена в таблице 10.
Таблица 10
| R | s0 | | |
| q1 | s0Пq2 | |Пq1 |
| q2 | s0Пq2 | |Пq3 |
| q3 | s0Лq0 | |Пq3 |
Задача 6.
Примените машину R к ленте
| s0 | | | | | | | s0 | s0 | | | | | s0 | | | | | s0 | s0 | s0 | |
| q1 |
Пример 8.
Машина L, отправляясь от воспринятого в стандартном положении числа, не самого левого на ленте, идет влево к стандартному положению ближайшего слева числа.
Задача 7.
Составьте программу машины L и проверьте ее работу на ленте
| s0 | | | | | | | s0 | s0 | | | | | s0 | | | | | s0 | s0 | s0 | |
| q1 |
Пример 9.
Рассмотрим машину Тьюринга, производящую следующую операцию: если на ленте дан набор чисел x1, x2, ..., xn, воспринимаемый машиной в стандартном положении, то машина в заключительном состоянии имеет на ленте набор чисел x1, x2, ..., xn, 3, воспринимаемый ею также в стандартном положении.
Так работает машина с программой, данной в таблице 11.
Таблица 11
| s0 | | | |
| q1 | s0Пq2 | |Пq1 |
| q2 | |Нq3 | |
| q3 | |Нq4 | |Пq3 |
| q4 | |Нq5 | |Пq4 |
| q5 | |Нq0 | |Пq5 |
Задача 8.
Проимитируйте работу машины для записи на ленте
| s0 | | | | | s0 | | | | | | | s0 | | | s0 | s0 | s0 | s0 | s0 | s0 |
| q1 |
Пример 10.
Рассмотрим машину Тьюринга, которая по записи любого числа на ленте распознает, оно больше нуля или равно нулю. В первом случае машина в качестве результата выдает число 1, записанное через одну пустую клетку справа от воспринимаемого числа, во втором — число 0, записанное также через одну пустую клетку справа от воспринимаемого числа.
Составим сначала схему работы этой машины (рис.).
| Иди на одну ячейку влево |
| В воспринимаемой ячейке стоит буква | |
| Иди на одну ячейку вправо |
| Через одну пустую ячейку от воспринимаемого числа напечатай |
| В пустой ячейке справа от | напечатай |
| Иди на одну ячейку вправо |
| Через одну пустую ячейку от воспринимаемого числа напечатай |
| остановись |
| Да |
| Нет |
В соответствии с этой схемой получим программу машины (табл. 12).
Таблица 12
| s0 | | | |
| q1 | s0Лq2 | |Лq2 |
| q2 | s0Нq3 | |Нq6 |
| q3 | s0Пq4 | |Пq4 |
| q4 | s0Пq5 | |Пq4 |
| q5 | |Нq0 | |
| q6 | s0Пq7 | |Пq7 |
| q7 | s0Пq8 | |Пq7 |
| q8 | |Нq9 | |
| q9 | |Нq0 | |Пq9 |
Задача 9.
Проимитируйте работу машины для записи на ленте:
a)
| s0 | | | | | s0 | s0 |
б)
| s0 | | | s0 | s0 | s0 |
Пример 11.
Построим машину, которая, отправляясь от числа, воспринятого в стандартном положении, стирает все числа левее данного (если таковые имеются) до первого встречного промежутка из двух или более пустых ячеек и возвращается к стандартному положению первоначально воспринятого числа.
Для построения программы такой машины (по существу, «построить машину Тьюринга» означает построить ее программу) составим по аналогии с примером 10 схему работы этой машины (рис.).
| Иди левее воспринимаемого числа на две ячейки |
| В воспринимаемой ячейке стоит буква s0 |
| Иди справа к стандартному положению ближайшего справа числа |
| Сотри все палочки слева до ближайшей слева пустой ячейки |
| остановись |
| Да |
| Нет |
Составим программу для этой машины (табл. 13).
Таблица 13
| s0 | | | |
| q1 | s0Лq2 | |Лq1 |
| q2 | q3 | q6 |
| q3 | s0Пq4 | |
| q4 | s0Пq4 | |Пq5 |
| q5 | s0Лq0 | |Пq5 |
| q6 | s0Нq1 | s0Лq6 |
Задача 10.
Проимитируйте работу машины с такой программой (табл. 13) для исходной записи на ленте:
| | | s0 | s0 | | | | | | | s0 | | | | | | | | | s0 | | | | | s0 |
| q1 |
Из примеров 9, 10, 11 видно, что для решения даже простых задач нужны довольно сложные машины Тьюринга. Естественно возникает вопрос: нельзя ли «собрать», сконструировать машины Тьюринга путем соединения нескольких более простых, элементарных машин?
В примере 9 мы могли бы поместить одну за другой машину С и три машины А.
В примерах 10, 11 мы могли бы сначала сконструировать машины для частных задач и затем «собрать» из них нужную машину. Из этих примеров видно также, что наряду с простым соединением машин (когда машина М' должна работать независимо от того, какая буква стояла в последней обозреваемой ячейке перед остановкой М) была бы желательна возможность и их дифференцированного соединения, т.е. такого, что если в последней обозреваемой ячейке перед остановкой машины М стояла буква s0, то дальше должна работать машина М1, иначе, т. е. если там стояла буква |, — то машина M2.
Даны две машины Тьюринга М1 и М2, имеющие общий алфавит А = {s0, s1, s2, …, sk} и состояния q0, q1, q2, ..., qp и q'0, q'1, q'2, ..., q'm соответственно. Композицией машин M1 и M2 называется машина, обозначаемая М1°М2, имеющая алфавит А и состояния q1, q2, ..., qp, q'1, q'2, ..., q'm, q'0 (начальное состояние машины M1°M2 - начальное состояние машины M1, т.е. q1, заключительное состояние - заключительное состояние машины М2, т.е. q'0).
Программа этой машины строится из программ машин М1 и M2 (см. табл. 14).
Таблица 14
| программа машины M2 |
| программа машины M1, заключительное состояние которой q0 заменено на состояние q'1 |

В соответствии с этим определением машину из примера 9 мы могли бы записать так: ((С°А)°А)°А.
Задача 11.
а) Покажите, что операция композиции машин ассоциативна, т.е. для любых машин M1, M2, M3
(M1°М2)°М3 = М1°(М2°М3).
б) Является ли операция композиции машин коммутативной?
Окончательно машину из примера 9 мы можем записать: С°А°А°А или С°А3, если условиться считать 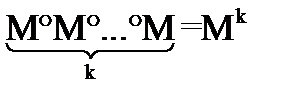
Даны 3 машины М1, М2, М3, имеющие общий алфавит А = {s0, s1, s2, ..., sk} и состояния q0, q1, ..., qp; q'0, q'1, ..., q'm; q''0, q''1, ..., q''n соответственно. Ветвлением машин M1, M2, М3 называется машина, обозначаемая 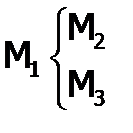 имеющая алфавит А и состояния q0, q1, q2, ..., qp, qp+1, q'1, ..., q'm, q''1, q''2, ..., q''n. Программа этой машины строится из программ машин M1, M2, M3 так, как показано в следующей таблице:
имеющая алфавит А и состояния q0, q1, q2, ..., qp, qp+1, q'1, ..., q'm, q''1, q''2, ..., q''n. Программа этой машины строится из программ машин M1, M2, M3 так, как показано в следующей таблице:
| программа машины М3, заключительное состояние которой q''0 заменено на q0 |
| программа машины М2, заключительное состояние которой q'0 заменено на q0 |
| команда условного перехода |
| программа машины M1, заключительное состояние которой q0 заменено на состояние qp+1 |

Проиллюстрируем теперь программу машины из примера 10 (табл. 16).
Таблица 16
| s0 | | | ||||||||||
| q1 | s0Лq2 | |Лq2 | ||||||||||
| q2 | s0Нq3 | |Нq6 | ||||||||||
| q3 | s0Пq4 | |Пq4 | ||||||||||
| q4 | s0Пq5 | |Пq4 | ||||||||||
| q5 | |Нq0 | |||||||||||
| q6 | s0Пq7 | |Пq7 | ||||||||||
| q7 | s0Пq8 | |Пq7 | ||||||||||
| q8 | |Нq9 | |||||||||||
| q9 | |Нq0 | |Пq9 |
Программа машины из примера 10 запишется, как видно, следующим образом: 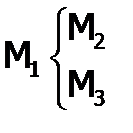 , где M1, M2, М3 указаны слева от программы.
, где M1, M2, М3 указаны слева от программы.
Дальнейший анализ программы машины из примера 10 показывает, что машина M1— это машина l, машину М2 можно представить в виде композиции машин r и С (r°С), а М3— в виде r°С°А. Тогда машина из примера 10 окончательно запишется так:
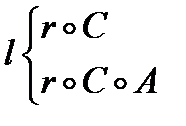
Как видно, из простых (элементарных) машин Тьюринга l, r, С, А с помощью операций композиции и ветвления сконструировали более сложную машину Тьюринга (пример 10).
Дана машина М, имеющая алфавит А={s0, s1, s2, ..., sk} и состояния q0, q1, …, qp. Программа машины М содержит по крайней мере две команды с заключительным состоянием q0. Будем говорить, что машина М' получена из машины М с помощью операции зацикливания, если в одной из команд машины М, содержащих состояние q0, это состояние заменено на одно из состояний q1, q2, …, qp.
Так, машина из примера 11 получена с помощью операции зацикливания из машины с программой, данной в таблице 17.
Таблица 17
| s0 | | | |
| q1 | s0Лq2 | |Лq1 |
| q2 | q3 | q6 |
| q3 | s0Пq4 | |
| q4 | s0Пq4 | |Пq5 |
| q5 | s0Лq0 | |Пq5 |
| q6 | s0Нq0 | s0Лq6 |
Действительно, эта программа содержит две команды с заключительным состоянием q0: s0Лq0 и s0Нq0. Заменив в команде s0Нq0 состояние q0 состоянием q1 получили машину из примера 11.
Проанализируем теперь программу этой машины, данную в таблице 18.
| машина Р, идущая на две ячейки влево от числа |
| команда условного перехода |
| машина R |
| машина Q, стирающая все единицы слева от ближайшей пустой ячейки |
| s0 | | | |
| q1 | s0Лq2 | |Лq1 |
| q2 | q3 | q6 |
| q3 | s0Пq4 | |
| q4 | s0Пq4 | |Пq5 |
| q5 | s0Лq0 | |Пq5 |
| q6 | s0Нq1 | s0Лq6 |
Работа этой машины может быть следующим образом описана в терминах машин Р, Q, R. Сначала используется машина Р, затем в соответствии с тем, обозревает машина Р в состоянии q2 пустую ячейку или ячейку с буквой |, используется машина R или Q соответственно. В случае если используется машина Q, ее результат подается в Р. Записать это можно следующим образом: 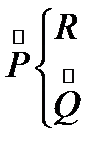 , где точки обозначают, что результат работы машины Q подается обратно в качестве входных данных для машины Р.
, где точки обозначают, что результат работы машины Q подается обратно в качестве входных данных для машины Р.
Пример 12.
Рассмотрим машину Тьюринга Т1, которая по записи любого числа, воспринятого в стандартном положении, по окончании работы через одну пустую ячейку от него выдает его копию, воспринимая ее в стандартном положении.
Машину Т1 построим, используя введенные ранее элементарные машины. Тогда:
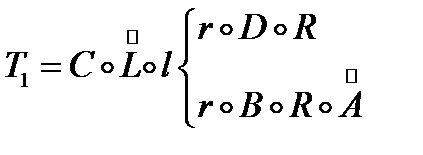
Задача 12.
а) Составьте программу машины Т1.
б) Имитируйте работу машины T1 для записи на ленте:
| s0 | s0 | | | | | | | s0 | s0 |
Порядок выполнения работы:
1. Изучить инструкцию к практической работе.
2. Выполнить задание.
3. Оформить отчет.
Содержание отчета:
1. Тема.
2. Цель.
3. Задачи.
4. Материальное обеспечение.
5. Практическое задание.
Вопросы для самопроверки
1. Где применяются система Тьюринга?
2. Чем превосходит алгоритм Марковой?
Практическая работа № 23
Тема: Решение задач по теории конечных автоматов. Таблицы, графы и матрицы переходов.
Цель: Научиться решать задачи по теории конечных автоматов.
Материальное обеспечение: практическая работа, программное обеспечение.
Дата добавления: 2019-02-22; просмотров: 489; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
