Производная функции, заданной параметрически
Производная обратной функции Рассмотрим функцию f(x), которая является строго монотонной на некотором интервале (a,b). Если в этом интервале существует точка x0, такая, что f′(x0)≠0, то функция x=φ(y), обратная к функции y=f(x), также дифференцируема в точке y0=f(x0) и ее производная равнаφ′(y0)=1f′(x0).Докажем приведенную теорему о производной обратной функции. Пусть переменная y получает в точке y0 приращение Δy≠0. Соответствующее ему приращение переменнойx в точке x0 обозначим как Δx, причем Δx≠0 в силу строгой монотонности функции y=f(x). Запишем отношение приращений в видеΔxΔy=1ΔyΔx.Допустим, что Δy→0. Тогда Δx→0, поскольку обратная функция x=φ(y) является непрерывной в точке y0. В пределе, при Δx→0, правая часть записанного соотношения становится равнойlimΔx→01ΔyΔx=1limΔx→0ΔyΔx=1f′(x0).В таком случае левая часть также стремится к пределу, который по определению равен производной обратной функции:limΔy→0ΔxΔy=φ′(y0).Таким образом,φ′(y0)=1f′(x0),то есть производная обратной функции равна обратной величине производной исходной функции. В приведенных ниже примерах найти производную заданной функции y=f(x) с помощью производной обратной функции x=φ(y). Пример 1 y=n√x Решение. Определим сначала обратную функцию для заданной функции y=n√x. Для этого выразим переменную xчерез y:y=f(x)=n√x,⇒yn=(n√x)n,⇒x=φ(y)=yn.По теореме о производной обратной функции можно записать:(n√x)′=f′(x)=1φ′(y)=1(yn)′=1nyn−1.Теперь вместо y подставляем y=n√x. В результате получаем выражение для производной заданной функции:(n√x)′=1nyn−1=1n(n√x)n−1=1nn√xn−1(x>0). Пример 2 y=arcsinx Решение. Функция арксинус является обратной к функции синус. Поэтому x=φ(y)=siny. Тогда производная арксинуса равна(arcsinx)′=f′(x)=1φ′(y)=1(siny)′=1cosy=1√1−sin2y=1√1−sin2(arcsinx)=1√1−x2,где −1<x<1. Пример 3 y=lnx Решение. Натуральный логарифм и экспоненциальная функция являются взаимно-обратными функциями. Следовательно, x=φ(y)=ey, где x>0, y∈R. Производную натурального логарифма легко вычислить через производную экспоненциальной функции:(lnx)′=f′(x)=1φ′(y)=1(ey)′=1ey=1elnx=1xЗдесь мы воспользовались основным логарифмическим тождеством, согласно которомуelnx=x. Пример 4 y=3√x+1 Решение. Найдем сначала обратную функцию x=φ(y) для заданной функции y=f(x), которая является монотонно возрастающей при любых x∈R. Выразим x через y:y=3√x+1,⇒y3=x+1,⇒x=y3−1.Теперь найдем производную f′(x):(3√x+1)′=f′(x)=1φ′(y)=1(y3−1)′=13y2=133√(x+1)2(x≠1). Пример 5 y=arccos(1−2x) Решение. Функция арккосинус определена и монотонна на отрезке [−1,1]. Следовательно, область определения исходной функции имеет вид:−1≤1−2x≤1,⇒−2≤−2x≤0,⇒0≤x≤1.Запишем обратную функцию x=φ(y):y=arccos(1−2x),⇒1−2x=cosy,⇒2x=1−cosy,⇒x=12−12cosy.Вычислим производную исходной функции через производную обратной функции:(arccos(1−2x))′=f′(x)=1φ′(y)=1(12−12cosy)′=112siny=2siny=2√1−cos2y=2√1−cos2(arccos(1−2x))=2√1−(1−2x)2=2√1−(1−4x+4x2)=2√1−1+4x−4x2=22√x−x2=1√x−x2.Заметим, что производная не определена в граничных точках x=0 и x=1 области определения функции y=f(x). Пример 6 y=√1+√x Решение. Данная функция определена и монотонно возрастает при x>0. Поэтому на этом интервале можно построить обратную функцию. Выразим x через y:y=√1+√x,⇒y2=1+√x,⇒√x=y2−1,⇒x=(y2−1)2.Теперь определим производную заданной функции y=f(x), используя теорему о производной обратной функции:(√1+√x)′=f′(x)=1φ′(y)=1[(y2−1)2]′=12(y2−1)⋅(y2−1)′=12(y2−1)⋅2y=14y(y2−1).Подставим вместо y выражение для исходной функции:(√1+√x)′=14y(y2−1)=14√1+√x((√1+√x)2−1)=14√1+√x(1+√x−1)=14√x√1+√x(x>0). Пример 7 y=arctan1x Решение. Обратная функция для данной функции имеет такой вид:y=arctan1x,⇒1x=tany,⇒x=1tany,гдеx≠0.Найдем производную исходной функции y=f(x):(arctan1x)′=f′(x)=1φ′(y)=1(1tany)′=1(−1tan2y)⋅1cos2y=−tan2y1cos2y.Воспользуемся тригонометрическим тождеством1cos2y=1+tan2y.Тогда(arctan1x)′=−tan2y1cos2y=−tan2y1+tan2y=−tan2(arctan1x)1+tan2(arctan1x)=−(1x)21+(1x)2=−1x2x2+1x2=−11+x2.Видно, что производная функции y=arctan1x отличается лишь знаком от производной функцииy=arctanx. Пример 8 y=√x Решение. Данная функция является обратной к квадратичной функции x=φ(y)=y2. Поэтому ее производная равна√x=f′(x)=1φ′(y)=1(y2)′=12y=12√x(x>0). Пример 9 y=2x+4 Решение. Запишем функцию x=φ(y), обратную к заданной функции y=f(x):y=2x+4,⇒2x=y−4,⇒x=y2−2.Тогда производная f′(x) имеет следующий вид:(2x+4)′=f′(x)=1φ′(y)=1(y2−2)′=11/2=2. Пример 10 Дана функция y=x5+2x3+3x. Найти производную обратной функции в точке x=1. Решение. В данном примере прямое вычисление обратной функции и ее производной будет слишком громоздким. Поэтому мы вычислим значение производной исходной функции в заданной точке и затем найдем обратную величину.y′=f′(x)=(x5+2x3+3x)′=5x4+6x2+3.Значение производной f′(x) при x=1 равно:f′(x=1)=5⋅14+6⋅12+3=14.Сама функция в точке x=1 принимает значение, равноеy(x=1)=15+2⋅13+3⋅1=6.По теореме о производной обратной функции получаемφ′(y=6)=1f′(x=1)=114. Пример 11 Дана функция y=x2−x. Найти производную обратной функции при x=1. Решение. Найдем производную исходной функцииy′=f′(x)=(x2−x)′=2x−1.Заметим, что точка x=12 разделяет области убывания (x<12) и возрастания (x>12) исходной функции. Каждому интервалу монотонности соответствует своя обратная функция, которые обозначим как φ1(y) и φ2(y). Выражения для этих функций можно получить в явном виде, решив уравнение y=f(x)относительно x:y=x2−x,⇒x2−x−y=0,⇒D=1+4y,⇒φ1,2(y)=1±√1+4y2.Производная обратной функции определяется по формулеφ′(y)=1f′(x)=12x−1(x≠12).Подставляя явные выражения x=φ1(y) и x=φ2(y) для обеих ветвей обратной функции, имеем:φ1′(y)=12(1+√1+4y2)−1=11+√1+4y−1=1√1+4y,φ2′(y)=12(1−√1+4y2)−1=11−√1+4y−1=−1√1+4y.Точка x=1 соответствует значению y=12−1=0 и находится на ветви φ2(y) обратной функции. Производная обратной функции в этой точке составляетφ2′(x=1)=φ2′(y=0)=−1√1+4⋅0=−1. Пример 12 Дана функция y=ex+2x+1. Найти производную обратной функции при x=0. Решение. При x=0 заданная функция принимает значениеy(x=0)=e0+2⋅0+1=2.Производная функции y=f(x) и ее значение в точке x=0 равныy′=f′(x)=(ex+2x+1)′=ex+2,y′(x=0)=f′(x=0)=e0+2=3.По теореме о производной обратной функции находимφ′(y=2)=1f′(x=0)=13. Пример 13 Для функции y=sin(x−1)+x2 найти производную обратной функции в точке x=1. Решение. Вычислим значение исходной функции и ее производной при x=1:y(x=1)=sin0+12=1,y′(x)=f′(x)=[sin(x−1)+x2]=cos(x−1)+2x,y′(x=1)=f′(x=1)=cos0+2⋅1=3.Отсюда находим значение производной обратной функции x=φ(y):φ′(y=1)=1f′(x=1)=13. Пример 14 Найти производную обратной функции для y=x2+2lnx и вычислить ее значение в точке x=1. Решение. Исходная функция y=f(x) определена при x>0. В этой области ее производная положительна:y′=f′(x)=(x2+2lnx)′=2x+2x>0приx>0.Следовательно, функция является монотонно возрастающей и для нее существует обратная функция. По теореме о производной обратной функции имеемφ′(y)=1f′(x)=12x+2x=12x2+2x=x2(x2+1).В данном случае зависимость x(y) невозможно выразить в явном виде. Однако из полученной формулы легко определить значение производной обратной функции при x=1. Предварительно вычислим соответствующее значение y:y(x=1)=12+2ln1=1+0=1.Тогдаφ′(y=1)=1f′(x=1)=12(12+1)=14. Пример 15 Найти производную обратной функции для y=x3−3x и вычислить ее значение при x=−2. Решение. Судя по производной:y′=f′(x)=(x3−3x)′=3x2−3=3(x2−1),функция имеет три интервала монотонности: 1. x∈(−∞,−1)− функция возрастает; 2. x∈(−1,1)− функция убывает; 3. x∈(1,∞)− функция возрастает. Каждому интервалу можно сопоставить свою обратную функцию. Далее мы считаем, что рассматривается обратная функция, соответствующая первому интервалу, который содержит точку x=−2. Производная обратной функции имеет вид:φ′(y)=1f′(x)=13(x2−1).Сама функция при x=−2 равнаy(x=−2)=(−2)3−3⋅(−2)=−8+6=−2.Тогда значение производной обратной функции в указанной точке составляетφ′(y=−2)=1f′(x=−2)=13⋅((−2)2−1)=19. Пример 16 Найти производную обратной функции для y=2x3−1 и вычислить ее значение при x=2. Решение. Вычислим производную заданной функции:y′=f′(x)=(2x3−1)′=6x.Видно, что производная меняет знак при переходе через точку x=0, т.е. функция убывает при x<0 и возрастает при x>0. Далее мы рассмотрим ветвь, включающую точку x=2. В этой области существует обратная функция. Ее производная определяется по формулеφ′(y)=1f′(x).Учитывая, что y(x=2)=2⋅23−1=15, получаемφ′(y=15)=1f′(x=2)=16⋅2=112. Пример 17 y=log2(x3) Решение. Функция y=f(x)=log2(x3) определена при x>0 и монотонно возрастает на этом интервале. Следовательно, она имеет обратную функцию x=φ(y):y=log2(x3),⇒x3=2y,⇒x=3⋅2y.По теореме о производной обратной функции находим:[log2(x3)]′=f′(x)=1φ′(y)=1(3⋅2y)′=13⋅2y⋅ln2=13ln2⋅2log2(x3)=13ln2⋅x3=1xln2.Здесь мы использовали основное логарифмическое тождествоalogax=x. Пример 18 Найти значение производной арксеканса y=arcsec x при x=√2. Решение. Воспользуемся тем, что арксеканс является обратной функцией для секанса. Будем считать, что выражение для производной секанса известно:(secy)′=tanysecy=sinycos2y.Учтем, что секанс принимает значение √2 в точке y=π4:sec(y=π4)=1cosπ4=1√22=√2.Тогда по теореме о производной обратной функции получаем(arcsec x)′=f′(x)=1φ′(y)=1(secy)′=1tanysecy=cos2ysiny.Соответственно, значение производной арксеканса в точке x=√2 равно:f′(x=√2)=1φ′(y=π4)=cos2π4sinπ4=(√22)2(√22)=√22. Пример 19 Найти производную функции обратной к функции y=x⋅3x при условии x>0. Решение. Вычислим производную заданной функции:y′=f′(x)=(x⋅3x)′=x′⋅3x+x⋅(3x)′=1⋅3x+x⋅3xln3=3x(1+xln3).Видно, что производная положительна при x>0. Следовательно, в этой области функция монотонно возрастает и для нее существует обратная функция x=φ(y). Производная обратной функции выражается формулойφ′(y)=1f′(x)=13x(1+xln3). Пример 20 Найти производную функции y=arcsinh x (обратный гиперболический синус). Решение. Функции y=arcsinh x (обратный гиперболический синус) и x=sinhy (гиперболический синус) являются взаимно-обратными. Поэтому, по теореме о производной обратной функции имеем:(arcsinh x)′=f′(x)=1φ′(y)=1(sinhy)′=1coshy.Выразим coshx через sinhx, используя соотношениеcosh2y−sinh2y=1(аналог основного тригонометрического тождества для гиперболических функций). Отсюда находимcosh2y=1+sinh2y,⇒coshy=√1+sinh2yУчитывая, что sinh(arcsinh x)=x, получаем следующее выражение для производной обратного гиперболического синуса:(arcsinh x)′=1coshy=1√1+sinh2y=1√1+sinh2(arcsinh x)=1√1+x2.
|
|
|
|
|
|
|
|
|
|
|
|
Производная функции, заданной параметрически
Определение
Предположим, что функциональная зависимость 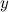 от
от  не задана непосредственно
не задана непосредственно 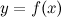 , а через промежуточную величину —
, а через промежуточную величину — 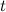 . Тогда формулы
. Тогда формулы
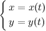
задают параметрическое представление функции одной переменной.
Пусть функция 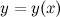 задана в параметрической форме, то есть в виде:
задана в параметрической форме, то есть в виде:
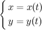
где функции 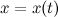 и
и 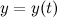 определены и непрерывны на некотором интервале изменения параметра
определены и непрерывны на некотором интервале изменения параметра 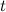 . Найдем дифференциалы от правых и левых частей каждого из равенств:
. Найдем дифференциалы от правых и левых частей каждого из равенств:

Далее, разделив второе уравнение на первое, и с учетом того, что  , получим выражение для первой производной функции, заданной параметрически:
, получим выражение для первой производной функции, заданной параметрически:
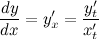
Для нахождения второй производной 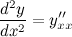 выполним следующие преобразования:
выполним следующие преобразования:
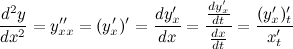
Пример
Задание. Найти вторую производную 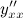 для функции
для функции 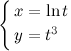 заданной параметрически.
заданной параметрически.
Решение. Вначале находим первую производную 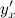 по формуле:
по формуле:
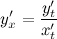
Производная функции 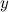 по переменной
по переменной 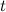 равна:
равна:
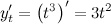
производная  по
по 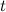 :
:
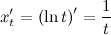
Тогда
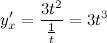
Вторая производная равна
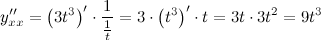
Ответ. 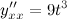
Дата добавления: 2019-02-22; просмотров: 337; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
