Построим вариационный ряд. Для этого сортируем ряд по возрастанию.
Задание 1.
На складе магазина имеется 15 коробок мороженого, 5 из них шоколадного. Найти вероятность того, что среди наудачу взятых 5 коробок мороженого окажутся 2 шоколадного.
Решение:
Для вычисления события A воспользуемся формулой 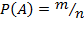 , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A.
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A.
В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно отобрать 5 коробок из 15, то есть  , а общее число благоприятствующих исходов равно числу способов, которыми можно отобрать 2 коробки шоколадного мороженого из 5, то есть
, а общее число благоприятствующих исходов равно числу способов, которыми можно отобрать 2 коробки шоколадного мороженого из 5, то есть  . То есть:
. То есть:
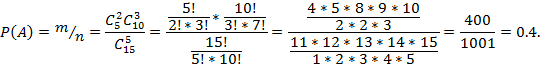
Задание 2.
В коробке конфет «Ассорти» находятся шоколадные конфеты с 4 видами начинок: «крем-брюле» – 50 %, с орехами – 20 %, с ликером – 20 %, «пралине» – 10 %. Какова вероятность того, что взятая наудачу конфета окажется с ликером или орехами?
Решение:
В коробке согласно условию лежит 20% конфет с ликером и 20% конфет с орехами. У нас есть только один шанс выбрать конфету, которая может оказаться с любой из начинок. Если предположить, что вероятность того, что мы вытащим конфету крем-брюле равна 50%, то бишь 0,5, с орехами равна 20%, то бишь 0,2, с ликёром равна 20%, то бишь 0,2, с пралине равна 10%, то бишь 0,1. Учитывая, что нам нужно найти вероятность того, что взятая наудачу конфета окажется с ликером или орехами, то используя формулу сложения вероятностей получим:
|
|
|
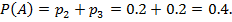
Задание 3.
Макаронные изделия изготавливаются на трех хлебозаводах. Первый завод производит 45 % общего количества макаронных изделий, второй – 40 %, третий – 15 %. Продукция первого завода содержит 70 % изделий высшего сорта, второго – 80 %, третьего – 81 %. В магазины поступают макаронные изделия со всех трех заводов. Какова вероятность того, что купленные в магазине макаронные изделия окажутся высшего сорта?
Решение:
В нашем случае мы имеем три несовместимых события. Рассмотрим следующие события:
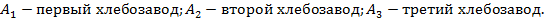
Согласно условиям, вероятность появления событий равны:
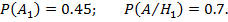
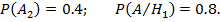
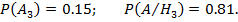
Найдем вероятности появления отдельного события:
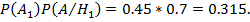
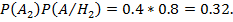
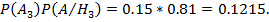
Используя формулу про полную вероятность имеем:
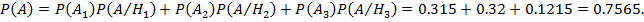
Задание 4.
В среднем 30 % изделий, выпускаемых предприятием, высшего сорта. Найти вероятность того, что среди 800 окажется не менее 5 и не более 280 изделий высшего сорта.
Решение:
За условием задачи:
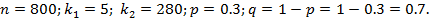
Для подсчета вероятности воспользуемся Интегральной теоремой Муавра – Лапласа:
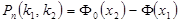 , де
, де 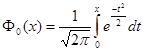 – функция Лапласа, значение аргумента -
– функция Лапласа, значение аргумента - 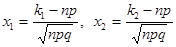 .
.
Найдем 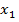 и
и 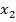 :
:
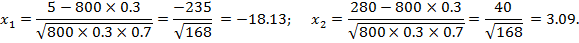
Значение аргументов берем с интегральной таблицы Лапласа:
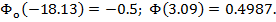
В конечном итоге имеем:
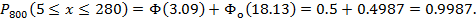
Задание 5.
Для заданной случайной величины 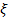 построить ряд распределения; найти функцию распределения
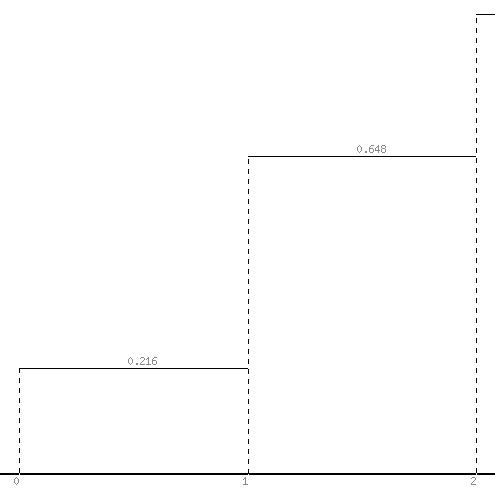
построить ряд распределения; найти функцию распределения  и построить ее график; вычислить характеристики M
и построить ее график; вычислить характеристики M 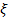 , D
, D 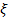 , σ
, σ 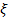 . На зачете студент получил 3 задачи. Вероятность решить каждую задачу равна 0,4. Случайная величина ξ – число решенных задач.
. На зачете студент получил 3 задачи. Вероятность решить каждую задачу равна 0,4. Случайная величина ξ – число решенных задач.
|
|
|
Решение:
Для того, чтоб найти закон распределения воспользуемся биноминальным распределением:
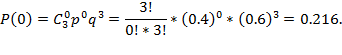
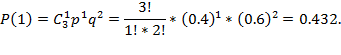

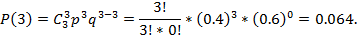
Имеем закон распределения случайно величины:

| 0 | 1 | 2 | 3 |
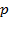
| 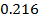
| 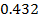
| 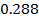
| 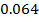
|
Функция распределения 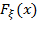 .
.
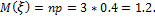
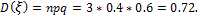
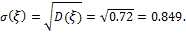
Задание 6.
Случайная величина 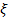 задана плотностью распределения вероятностей
задана плотностью распределения вероятностей 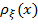 . Требуется определить постоянную C и найти функцию распределения )
. Требуется определить постоянную C и найти функцию распределения )  ; построить графики )
; построить графики ) 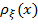 и
и  ; вычислить M
; вычислить M 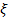 , D
, D 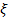 , σ
, σ 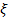 ,
, 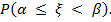
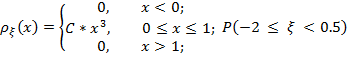
Решение:
Чтоб найти неизвестный параметр используем условие нормирование для непрерывной величины: 
Тогда, используя условие нормирования для непрерывной величины:

Тогда функция распределения будет иметь вид:
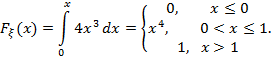
График функции  ; будет иметь вид:
; будет иметь вид:

Тогда плотность распределения будет иметь вид:
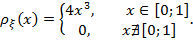
График функции 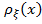 будет иметь вид:
будет иметь вид:
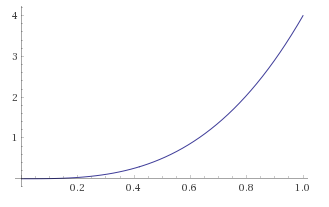
Рассчитаем числовые характеристики распределения:
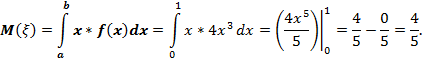
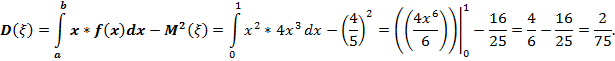
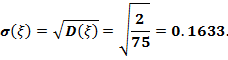
Вероятность того, что значение будет заключено в интервале:
|
|
|
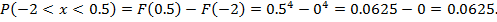
Задание 7.
Для исходной выборки:
а) определить вариационный ряд и размах выборки;
б) построить простую статистическую таблицу и полигон частот;
в) построить интервальную таблицу и гистограмму;
г) найти эмпирическую функцию распределения и построить ее график;
д) найти выборочную среднюю, выборочную и исправленную дисперсию.
Определялась жирность коровьего молока от 15 коров. Были получены следующие результаты (%): 3,68; 3,66;3,76; 3,78; 3,94; 3,88; 3,86; 3,88; 3,94; 4,00; 3,90; 4,18; 3,96; 4,35; 3,70.
Решение:
Построим вариационный ряд. Для этого сортируем ряд по возрастанию.
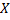
| 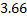
| 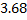
| 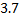
| 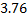
| 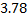
| 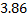
| 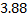
| 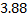
| 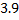
| 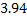
| 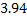
| 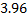
| 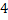
| 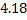
| 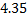
|
Разность между максимальным и минимальным элементами выборки называется размахом выборки .Определим размах выборки:
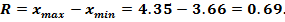
Статистическое распределение исходной выборки можно записать в виде следующей таблицы:
| 
| 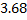
| 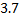
| 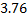
| 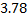
| 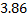
| 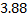
| 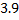
| 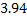
| 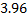
| 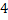
| 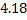
| 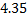
|
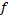
| 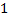
| 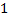
| 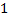
| 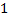
| 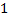
| 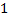
| 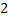
| 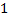
| 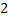
| 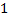
| 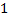
| 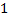
| 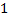
|
Построим полигон частот:
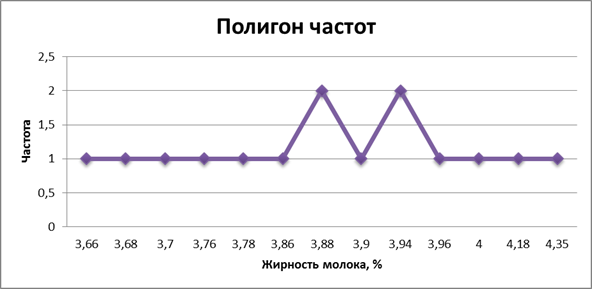
Рисунок 1. Полигон частот.
Построим интервальное распределение. Для этого определим с помощью формулы Стэрджесса количество интервалов:
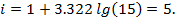
Ширина интервала:
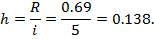
Тогда границы интервала будут:
| Группы | Середина интервала | Кол-во, fi |
| 3.66 - 3.8 | 3.73 | 5 |
| 3.8 - 3.94 | 3.87 | 6 |
| 3.94 - 4.08 | 4.01 | 2 |
| 4.08 - 4.22 | 4.15 | 1 |
| 4.22 - 4.36 | 4.29 | 1 |
| Итого | 15 |
|
|
|
На основе интервального распределения построим гистограмму частот:
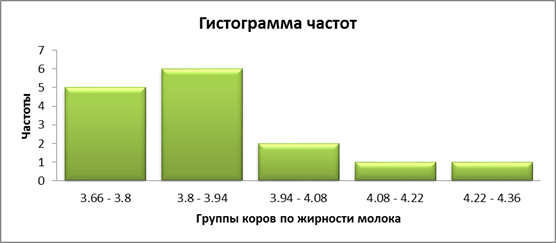
Рисунок 2. Гистограмма частот.
Найдем и построим функцию и график эмпирической функции распределения:
Функция распределения F(X).
F(x≤3.73) = 0
F(3.73< x ≤3.87) = 0.333
F(3.87< x ≤4.01) = 0.4 + 0.333 = 0.733
F(4.01< x ≤4.15) = 0.133 + 0.733 = 0.867
F(4.15< x ≤4.29) = 0.0667 + 0.867 = 0.933
F(x>4.29) = 1
Соответственно график будет иметь вид:
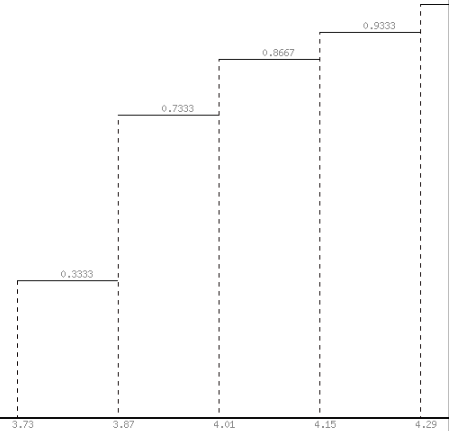
Рисунок 3. Эмпирическая функция распределения.
Найдем числовые характеристики распределения. Для этого построим вспомогательную таблицу:
| Группы | Середина интервала, xцентр | Кол-во, fi | xi * fi | |x - xср|*fi | (x - xср)2*fi |
| 3.66 - 3.8 | 3.73 | 5 | 18.65 | 0.793 | 0.126 |
| 3.8 - 3.94 | 3.87 | 6 | 23.22 | 0.112 | 0.00209 |
| 3.94 - 4.08 | 4.01 | 2 | 8.02 | 0.243 | 0.0294 |
| 4.08 - 4.22 | 4.15 | 1 | 4.15 | 0.261 | 0.0683 |
| 4.22 - 4.36 | 4.29 | 1 | 4.29 | 0.401 | 0.161 |
| Итого | 15 | 58.33 | 1.811 | 0.387 |
В качестве оценки математического ожидания используется среднее арифметическое 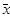 наблюденных значений. Эта статистика называется выборочным средним.
наблюденных значений. Эта статистика называется выборочным средним.
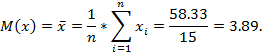
В качестве оценки дисперсии используется статистика:
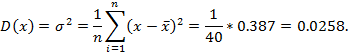
Среднее квадратическое отклонение:
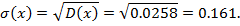
В качестве оценки исправленной дисперсии используется статистика:
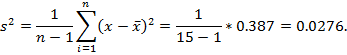
Оценка среднего квадратического отклонения:
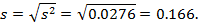
Задание 8.
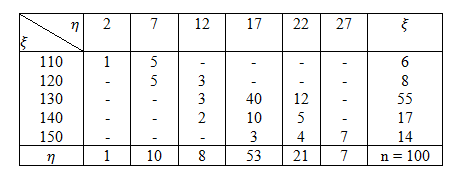
По корреляционной таблице найти уравнения прямых регрессий 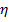 на
на 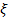 и
и 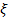 на
на  . Построить корреляционное поле и прямые регрессии. Оценить тесноту линейной связи в процентах.
. Построить корреляционное поле и прямые регрессии. Оценить тесноту линейной связи в процентах.
Решение:
Построим поле корреляции:

Уравнение линейной регрессии с  на
на  имеет вид:
имеет вид:
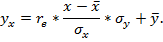
Уравнение линейной регрессии с  на 𝑦 имеет вид:
на 𝑦 имеет вид:

Найдем необходимые числовые характеристики.
Выборочные средние:
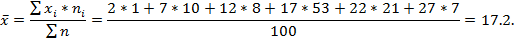
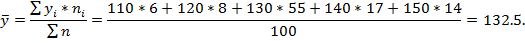
Выборочные дисперсии:
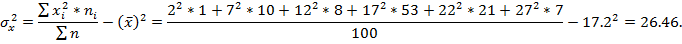

Выборочные среднеквадратическое отклонение:
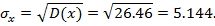
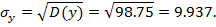
Определим коэффициент корреляции:
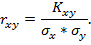
Найдем ковариацию:
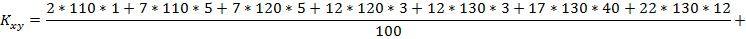
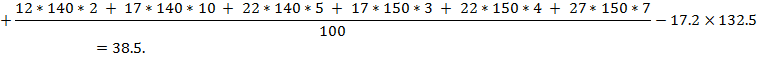
Коэффициент корреляции:
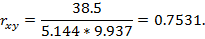
Дата добавления: 2019-02-22; просмотров: 302; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
