Малюнок 2.7. Програма як діалектичне заперечення проблеми 11 страница
Лема 4.18 Клас КВ-мов замкнений відносно дзеркального відображення (обернення) ланцюжків.
Дійсно, нехай КВ-мова L породжена граматикою G=(N, T, P, S). Тоді мова  буде породжена КВ-граматикою G=(N, T,
буде породжена КВ-граматикою G=(N, T, 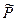 , S), де
, S), де 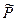 ={A→
={A→ 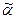 | A→αÎP}.
| A→αÎP}.
Визначимо операції дублювання та дзеркального дублювання наступним чином: D(L)={ ww | wÎL} та DM(L)={ w 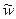 | wÎL}.
| wÎL}.
Лема 4.19 Клас КВ-мов не замкнений відносно операцій дублювання та дзеркального дублювання.
Для доведення цього факту достатньо розглянути приклад. Візьмемо КВ-мову L={anbn| n≥0}. Тоді мови D(L)={ anbnanbn| n≥0 } та DM(L)={ anb2nan| n≥0} не можуть бути КВ-мовами в силу леми про розростання.
Таким чином, клас КВ-мов не утворює підалгебру теоретико-множинної алгебри формальних мов, бо не є замкненим відносно перетину та доповнення. Тому для КВ-мов розглядаються інші алгебри, в першу чергу алгебра ACF={CF, È, ×} з операціями об’єднання та конкатенації. Алгебри з такими операціями будемо називати слабкими алгебрами формальних мов (САФМ). Виявляється, цих операцій достатньо для задання КВ-мов за допомогою рівнянь в цій алгебрі. Цей факт буде розглянуто пізніше.
4.11 Дерева виводу
Визначення 4.39 Нехай G = (N, Т, Р, S) — контекстно-вільна граматика і S 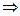 Gα1
Gα1 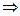 Gα2
Gα2 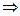 G...
G... 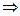 Gαn – вивід в G. Будемо називати цей вивід лівостороннім, якщо для кожного i, 0
Gαn – вивід в G. Будемо називати цей вивід лівостороннім, якщо для кожного i, 0  i<n, можемо записати αi у вигляді wiAiβi, αі+1 – wiγiβi, де Ai→γi ÎР, w i
i<n, можемо записати αi у вигляді wiAiβi, αі+1 – wiγiβi, де Ai→γi ÎР, w i  T* і Ai
T* і Ai  N. Змістовно, вивід є лівостороннім, якщо на кожному кроці заміняється найлівіший нетермінал.
N. Змістовно, вивід є лівостороннім, якщо на кожному кроці заміняється найлівіший нетермінал.
Очевидним є наступне твердження.
Лема 4.20 Нехай G = (N, Т, Р, S) — контекстно-вільна граматика. Якщо w  L(G), то існує лівосторонній вивід w в G.
L(G), то існує лівосторонній вивід w в G.
Визначення 4.40 Для контекстно-вільних граматик кожному виводу вигляду S 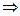 Gα1
Gα1 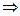 Gα2
Gα2 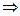 G...
G... 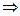 Gαn можна співставити скінченне впорядковане дерево, яке має назву дерева виводу. Вершини дерева відмічені символами алфавіту NÈТ. Корінь дерева відмічено початковим символом S. Якщо у виводі було застосовано правило S→α, то кожному символу ланцюжка α, на який замінюється символ S на першому кроці виводу, ставиться у відповідність вершина дерева, і до неї проводиться дуга із кореня. Отримані таким чином безпосередні нащадки кореня впорядковані відповідно до їх порядку у ланцюжку α. Для тих із одержаних вершин, що відмічені символами з множини N, робиться аналогічна побудова і т.д. Кроною дерева виводу називається слово, записане на вершинах, відмічених символами з алфавіту Т.
Gαn можна співставити скінченне впорядковане дерево, яке має назву дерева виводу. Вершини дерева відмічені символами алфавіту NÈТ. Корінь дерева відмічено початковим символом S. Якщо у виводі було застосовано правило S→α, то кожному символу ланцюжка α, на який замінюється символ S на першому кроці виводу, ставиться у відповідність вершина дерева, і до неї проводиться дуга із кореня. Отримані таким чином безпосередні нащадки кореня впорядковані відповідно до їх порядку у ланцюжку α. Для тих із одержаних вершин, що відмічені символами з множини N, робиться аналогічна побудова і т.д. Кроною дерева виводу називається слово, записане на вершинах, відмічених символами з алфавіту Т.
Приклад 4.25 Візьмемо наступну граматику для мови L=L 1ÈL 2, де L1={anbmcm | n,m³0} та L2={anbncm | n,m³0}:
S®AB | CD | e
A®e| aA
B®e| bB c
C®e| a C b
D®e| c D
Виводу SÞABÞAbB cÞa AbB cÞa Ab b B ccÞa Ab bb B cccÞa b bb B cccÞa b bbccc відповідає наступне дерево виводу:

Неважко довести таку лему.
Лема 4.21 Нехай G = (N, Т, Р, S) — контекстно-вільна граматика і w  L(G). Тоді існує взаємно-однозначна відповідність між лівосторонніми виведеннями слова w в граматиці G і деревами виводу в граматиці G, кроною яких є w.
L(G). Тоді існує взаємно-однозначна відповідність між лівосторонніми виведеннями слова w в граматиці G і деревами виводу в граматиці G, кроною яких є w.
Дерево виводу фактично задає клас еквівалентності виводів, які розрізняються лише порядком застосування правил. Тому для задач, для яких порядок застосувань не є важливим, доцільно спиратися на дерева виводу. Крім того, дерева виводу фактично задають структурну організацію ланцюжка, яка є важливою в різних застосуваннях граматик, зокрема, і в семантиці.
4.12 Однозначні та неоднозначні граматики
Визначення 4.41 КВ-граматика називається неоднозначною, якщо існує ланцюжок, котрий має два або більше різних лівосторонніх виводів. В противному випадку КВ-граматика називається однозначною.
Приклад 4.26 КВ-граматика із прикладу 4.25 неоднозначна. Слово aa b bcc має два різних лівосторонніх вивода:
SÞABÞa ABÞaa ABÞaa BÞaab B cÞaabbBccÞaabbcc
та
SÞCDÞaCbDÞaaCbbDÞaabbDÞaabdDcÞaabbDccÞaabbcc
Також неоднозначною є граматика (БНФ) мови SIPL, наведена в першому розділі.
Приклад 4.27 Мова Діка – це мова, що породжена граматикою Gk = ({S} , T , P , S), де k>0, T = {α1, α2,…, αk, b1, b2,…, bk} та Р складається з продукцій S→SS , S→ε , S→αiSbi, 1  i
i  k. Нехай Lk=L(Gk). Зрозуміло, що мова Діка є контекстно-вільною мовою. Можна вважати, що мова Діка – це множина усіх ланцюжків урівноважених дужок k різних типів, де ai та bi – це ліва та права дужки для кожного і. Мова Діка є важливою в теорії контекстно-вільних граматик. Вона, зокрема, утворює основу довільної контекстно-вільної мови, тому що будь-яка КВ-мова є гомоморфним образом мови Діка. Наведена граматика не є однозначною. Але наступна граматика
k. Нехай Lk=L(Gk). Зрозуміло, що мова Діка є контекстно-вільною мовою. Можна вважати, що мова Діка – це множина усіх ланцюжків урівноважених дужок k різних типів, де ai та bi – це ліва та права дужки для кожного і. Мова Діка є важливою в теорії контекстно-вільних граматик. Вона, зокрема, утворює основу довільної контекстно-вільної мови, тому що будь-яка КВ-мова є гомоморфним образом мови Діка. Наведена граматика не є однозначною. Але наступна граматика 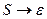 ,
, 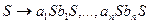 – однозначна.
– однозначна.
Визначення 4.42 КВ-мова називається суттєво неоднозначною, якщо кожна КВ-граматика, яка породжує цю мову, є неоднозначною.
Приклад 4.28 КВ-мова L=L 1ÈL 2 з прикладу 4.25, де L1={anbmcm | n,m³0} та L2={anbncm | n,m³0} є суттєво неоднозначною. Доведення цього факту наводиться в книзі [Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции] стор. 234-236.
Неоднозначність є важливим поняттям теорії мов. Якщо граматика, яка використовується для породження мови програмування, є неоднозначна, то це може призвести до її неоднозначної семантичної інтерпретації, що є небажаним явищем.
4.13 Розв’язні та нерозв’язні проблеми КВ-граматик та мов
Масову проблему називають алгоритмічно розв’язною, або розв’язною, якщо предикат, який її визначає, є рекурсивний, інакше проблему називають алгоритмічно нерозв’язною, або нерозв’язною.
Масову проблему називають частково алгоритмічно розв’язною, або частково розв’язною, або напіврозв’язною, якщо предикат, який її визначає, є частково рекурсивний.
Для КВ-граматик та мов наступні проблеми є розв’язними:
1. Чи є мова, породжувана КВ-граматикою, порожньою?
2. Чи є мова, породжувана КВ-граматикою, скінченною?
3. Чи є мова, породжувана КВ-граматикою, нескінченною?
4. Чи належить ланцюжок w мові, що породжується КВ-граматикою?
Для КВ-граматик та КВ-мов наступні проблеми є нерозв’язними.
1. Чи є перетин мов, породжуваних двома КВ-граматиками, порожнім?
2. Чи є перетин мов, породжуваних двома КВ-граматиками, скінченним?
3. Чи є перетин мов, породжуваних двома КВ-граматиками, нескінченним?
4. Чи є КВ-граматика однозначною?
5. Чи є порожнім (скінченним, нескінченним) доповнення до КВ-мови?
6. Чи співпадає КВ-мова, породжувана граматикою, з T*?
7. Чи є еквівалентними дві КВ-граматики?
8. Чи є регулярною мова, породжувана КВ-граматикою?
Зазначимо, що проблеми, розв’язні для КВ-граматик та мов будуть розв’язними і для регулярних граматик та мов. Разом з тим, деякі проблеми, нерозв’язні для КВ-граматик та мов, можуть бути розв’язними для регулярних граматик та мов. Зокрема, такими є вищенаведені проблеми 1-7, переформульовані на випадок регулярних граматик та мов.
4.14 Рівняння в алгебрах формальних мов
Граматики та БНФ є формалізмами, що задають мову «поштучно», «поелементно», вказуючи механізм породження окремих слів. Разом з тим, сама форма граматик та БНФ підштовхує до думки, що їх можна розглядати як системи рівнянь, розв’язками яких є мови. Щоб перейти до такого тлумачення, попередньо введемо необхідні визначення.
Визначення 4.43 Слабкою алгеброю формальних мов над алфавітом T будемо називати алгебру AL=(2T*, È, ·) з операціями об’єднання та добутку мов.
Визначення 4.44 Множиною виразів LExp над множиною змінних Var називається множина, задана наступним індуктивним визначенням:
1) якщо xÎ Var, то xÎ Lexp,
2) якщо LÍT*, то LÎLexp,
3) якщо t, t¢ÎLexp, то tÈt¢, t·t¢ÎLexp.
Визначення 4.45 Формальним рівнянням (формальною рівністю) над алгеброю AL називається запис вигляду t=t¢, де t, t¢ÎLexp.
Визначення 4.46 Інтерпретацією (означуванням, оцінкою) змінних називається довільне відображення n: Var®2T*. Інтерпретація змінних однозначно (та гомоморфно) продовжується до відображення mn: LExp®2T* інтерпретації виразів, параметром якого є інтерпретація змінних n, яке задається індуктивно за побудовою виразу eÎLexp:
1) якщо e =x (xÎVar), то mn(e)= n(x),
2) якщо e =L (L ÍT*), то mn(e)= L,
3) якщо e = tÈt¢, то mn(e)=mn(t)Èmn(t¢),
4) якщо e = t·t¢, то mn(e)=mn(t) · mn(t¢).
Визначення 4. 47 Наведене визначення дозволяє абстрагувати відображення mn до оператора m: LExp ® ((Var®2T*)®2T*). Вираз e, який містить змінні x 1, …, xn, будемо позначати e(x 1, …, xn), а відповідний оператор – m( e(x 1, …, xn)).
Приклад 4.29 Нехай Var = {x, y, z}, n(x)={a,ab}, n(y)={e,b,cc}, n(z)={bb,c}. Тоді вираз x 2 z{a}y інтерпретується таким чином:
mn(x 2 z{a}y)={a,ab}2{bb,c}{a}{e,b,cc}={a a, a a b, aba, abab}{bb a,c a}{e,b,cc}=
{a a bb a, a a bbb a, aba bb a, abab bb a, a a c a, a a bc a, aba c a, abab c a}{e,b,cc} =
{a a bb a, a a bbb a, aba bb a, abab bb a, a a c a, a a bc a, aba c a, abab c a, b,cc} =
{a a bb ab, a a bbb ab, aba bb ab, abab bb ab, a a c ab, a a bc ab, aba c ab, abab c ab, a a bb acc, a a bbb acc, aba bb acc, abab bb acc, a a c acc, a a bc acc, aba c acc, abab c acc}
Визначення 4.48 Інтерпретація (означування) змінних n: Var®2T* називається розв’язком рівняння t=t¢, якщо mn(t)=mn(t¢).
Визначення 4.49 Розвязком системи рівнянь {t1=t¢1, …, t n=t¢n} є така інтерпретація змінних, яка кожне рівняння перетворює у рівність.
Визначення 4.50 Рівняння виду x=t, де xÎVar, tÎLexp називаєть рекурсивним. Якщо у виразі t фігурують лише скінченні мови, то рівняння називають слабкорекурсивним. Аналогічно вводяться понятя рекурсивних та слабко рекурсивних систем рівнянь.
Розв’язок рівнянь в алгебрах мов можна знаходити різними методами, але найважливішим є метод поступових наближень.
Приклад 4. 30
Розглянемо мову L={anbn | n³0}. Ця мова породжується наступною простою граматикою G: S®e | aSb.
Цій граматиці відповідає наступне рівняння: S={e}È{a}S{b}. Позначимо оператор m({e}È{a}S{b}(S)) як j(S).
Розв’язок рівняння знаходять методом послідовних наближень. Найперше наближення – порожня мова Æ. Наступні наближення отримуємо підстановкою в оператор j(S) замість S попереднього наближення. (Для спрощення тут можна говорити про підставку в саме рівняння). Отримуємо наступну послідовність наближень:
R(0)= Æ;
R(1)= {e};
R(2)= {e}È{ab}={e, ab};
R(3)= {e, ab}È{ab, aabb}={e, ab, aabb};
… … …
R(i+1)=R(i)È{a} R(i){b};
… … …
Вважаємо, що
R=ÈiÎw R(i).
(Тут w є першим граничним ординаром і може тлумачитись як множина натуральних чисел. Детальніше про це буде сказано у наступному розділі посібника.)
Використовуючи оператор j отримуємо, що R(i+1)=j( R(i)) та R=ÈiÎwj(R(i)). Мова R і буде розв’язком нашого рівняння.
Щоб це довести, розглянемо наступну властивість оператора j.
Лема 4. 22 (неперевність j ). j(ÈiÎw R(i))= ÈiÎw j(R(i)).
Доведення.
Спочатку доведемо, що j(ÈiÎw R(i))ÍÈiÎw j(R(i)). Дійсно, нехай xÎj(ÈiÎw R(i)). Тоді xÎ{e}, або xÎ{a}(ÈiÎw R(i)){b}. В першому випадку очевидно, що xÎÈiÎw j(R(i)). У другому випадку xÎj(R(i+1)), тому xÎÈiÎw j(R(i)).
Тепер доведемо, що j(ÈiÎw R(i))ÊÈiÎw j(R(i)). Нехай тепер xÎÈiÎw j(R(i)). Тоді існує kÎw таке, що xÎj(R(k)). Це означає, що xÎ{e}, або xÎ{a}(R(k-1)){b}. Тому xÎ{a}(ÈiÎw R(i)){b}, тобто xÎj(ÈiÎw R(i)). ▄
Дата добавления: 2019-02-13; просмотров: 248; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
