Теорема про існування частки та її єдність. Теорема про неможливість ділення на нуль.
Існування частки, її єдиність
Чи завжди існує частка натуральних чисел а і b? Відповідь на це запитання дає наступна теорема:
Теорема. Для того, щоб існувала частка двох натуральних чисел а і b, необхідно, щоб  .
.
Доведення. Нехай частка натуральних чисел а і b існує, тобто існує таке натуральне число с, що  . Для будь-якого натурального числа с правильне твердження
. Для будь-якого натурального числа с правильне твердження 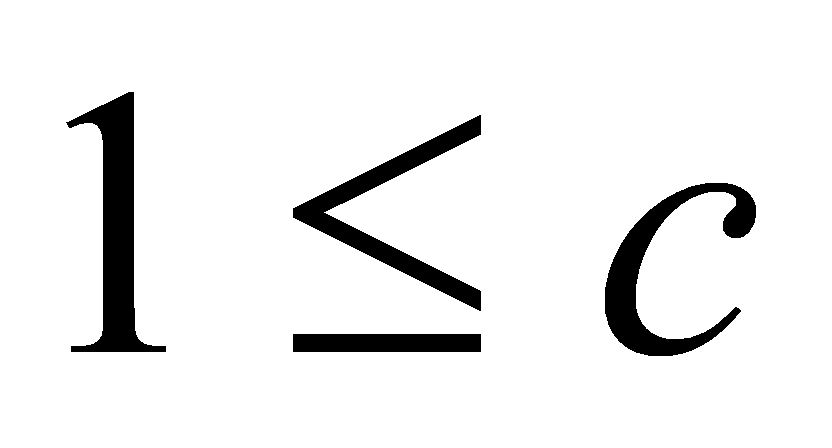 . Помножимо обидві частини цієї нерівності на натуральне число b, отримаємо
. Помножимо обидві частини цієї нерівності на натуральне число b, отримаємо 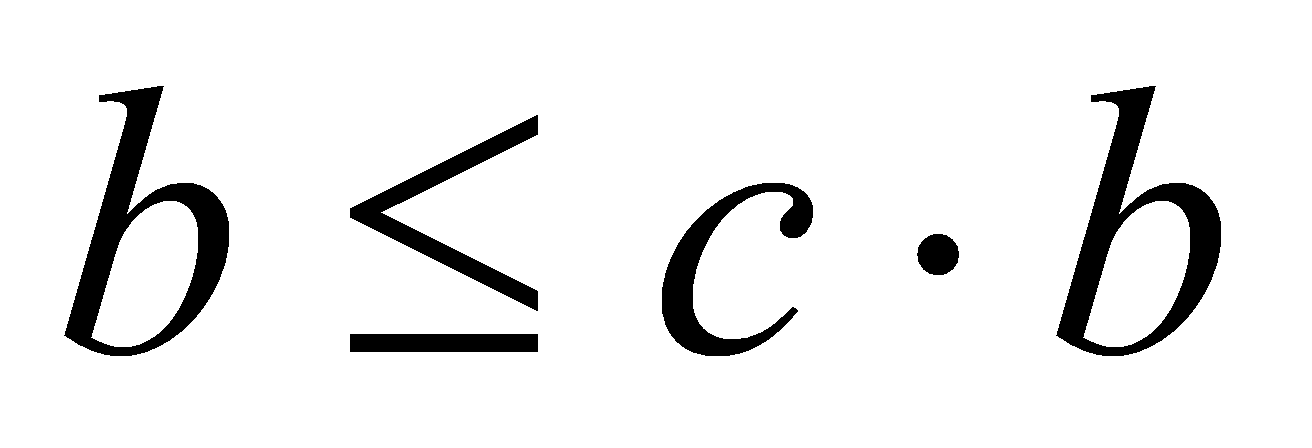 . Оскільки
. Оскільки 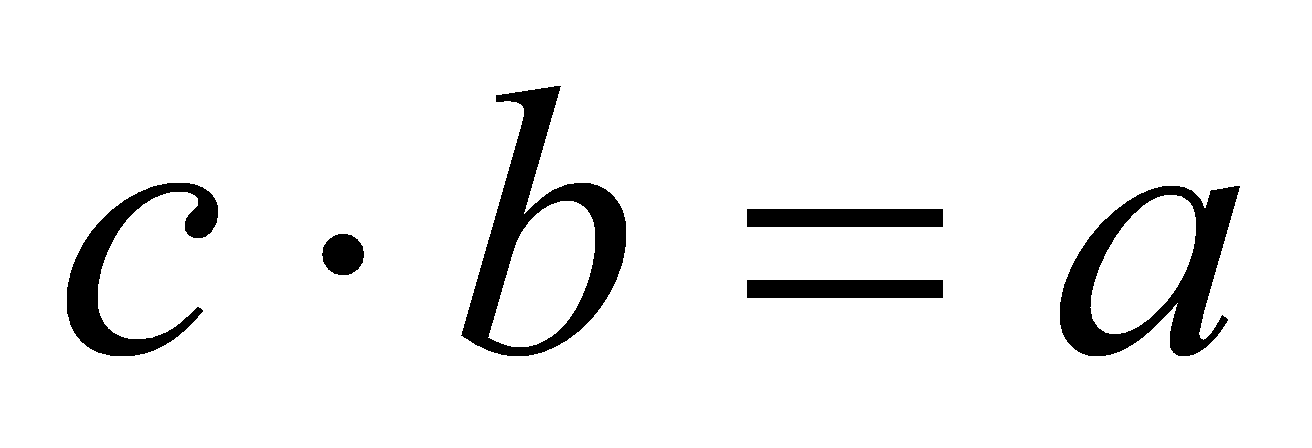 , то
, то  . Теорему доведено.
. Теорему доведено.
Чому дорівнює частка  і натурального числа b? За означенням це таке число а, яке задовольняє умові
і натурального числа b? За означенням це таке число а, яке задовольняє умові 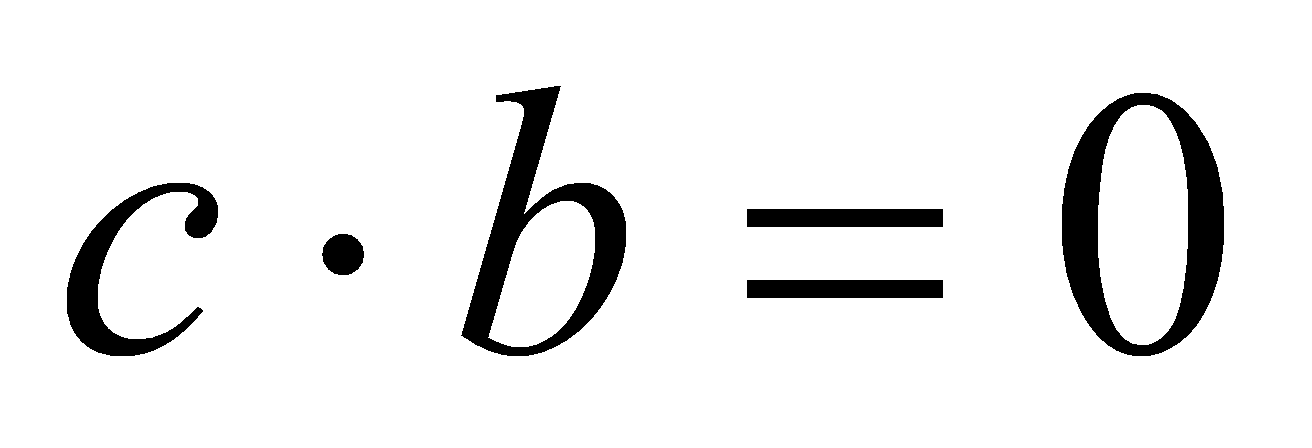 . Так як
. Так як 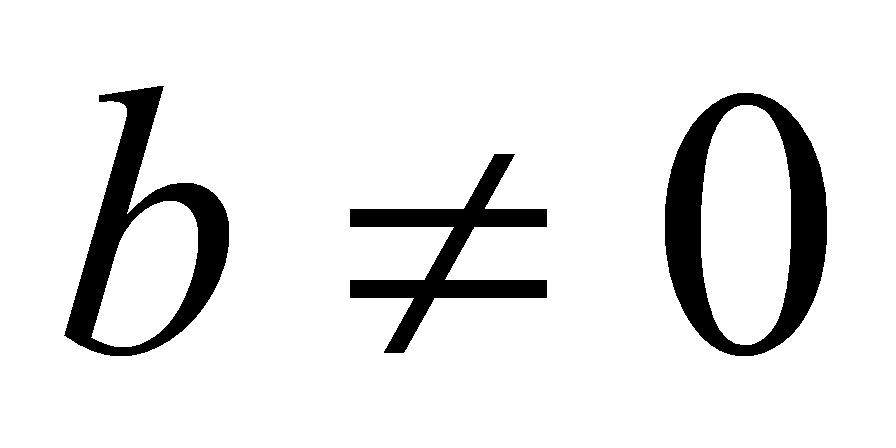 , то рівність
, то рівність 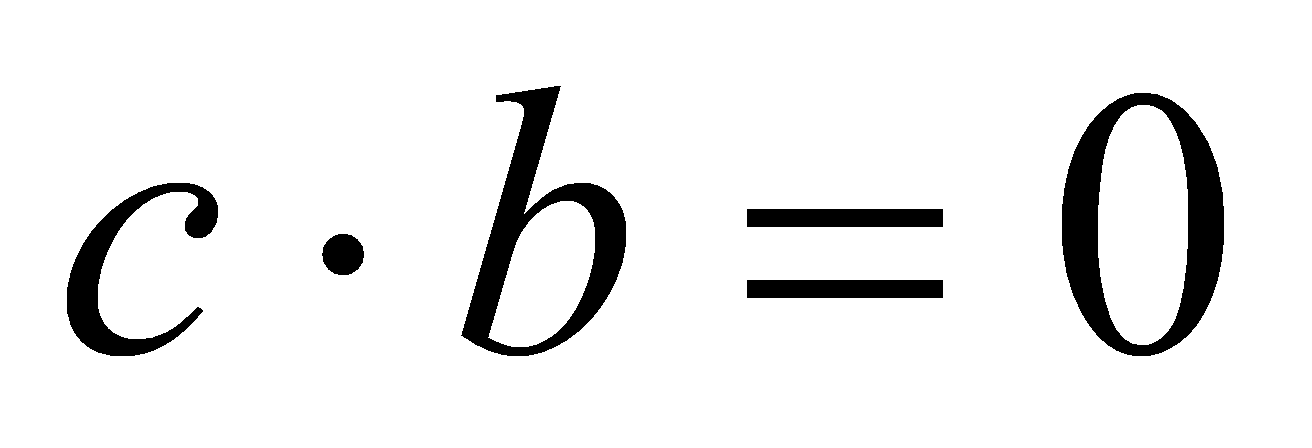 виконується, якщо
виконується, якщо  . Отже,
. Отже, 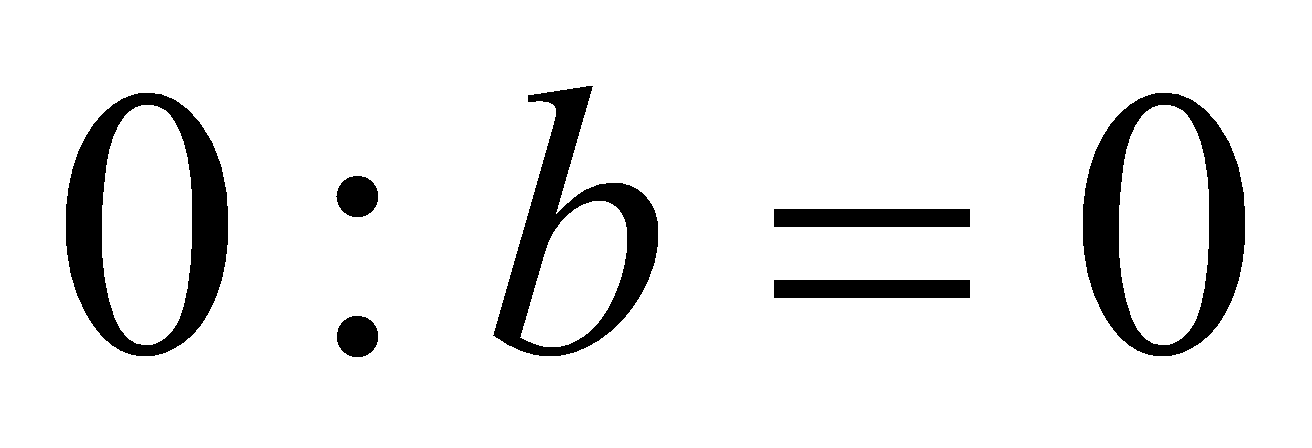 , якщо
, якщо 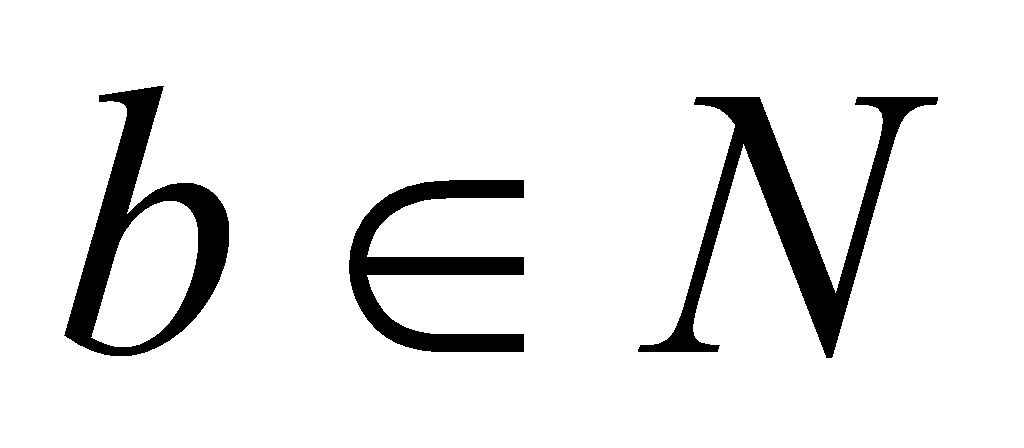 .
.
Теорема. Якщо частка натуральних чисел існує, то вона єдина.
Доведення (методом від супротивного). Припустимо, що існують дві частки 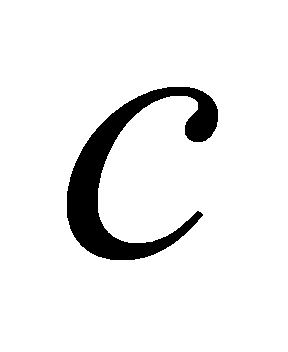 і
і 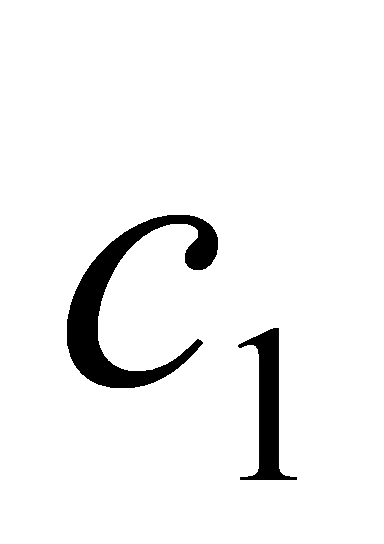 , тобто
, тобто 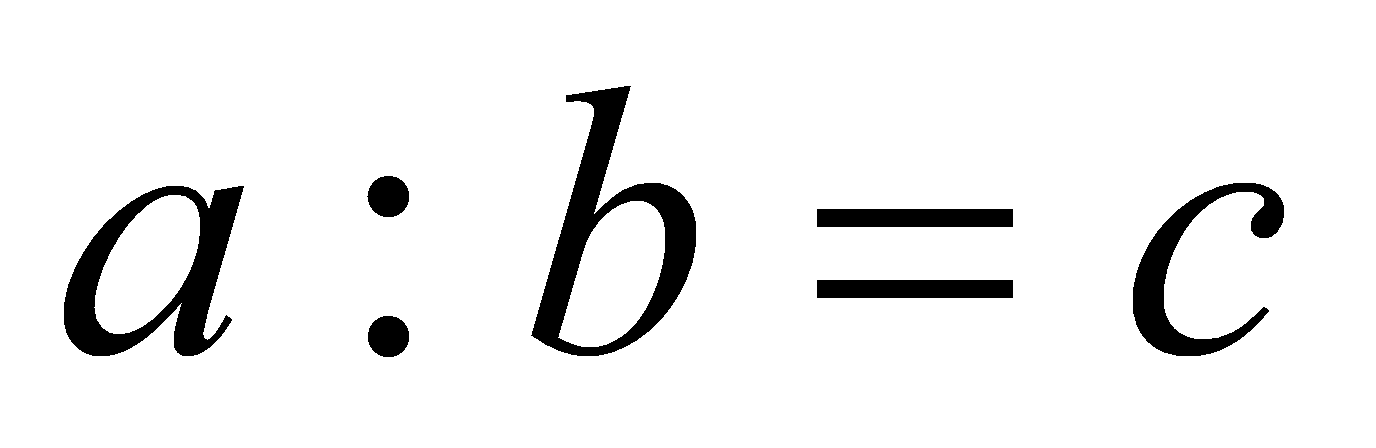 і
і 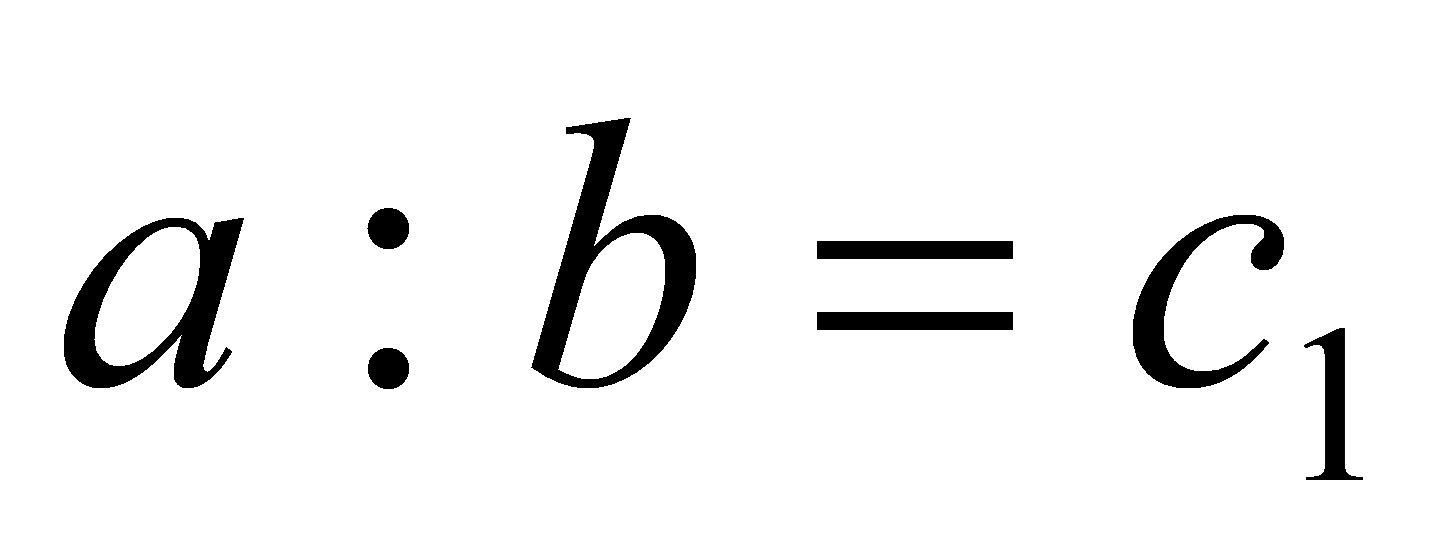 . Нехай, наприклад,
. Нехай, наприклад, 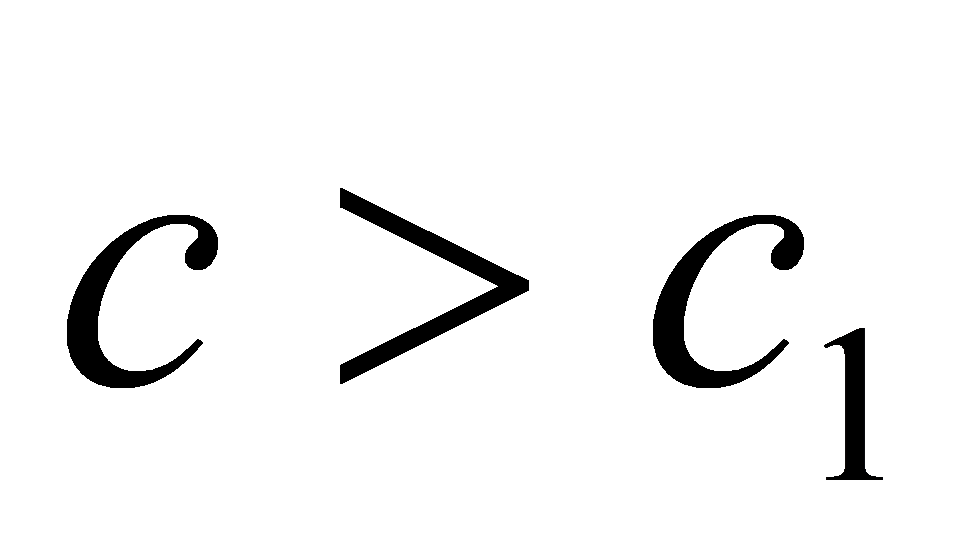 . Проте це суперечить властивості монотонності дії множення натуральних чисел. Отже, наше припущення, що існують два різних числа
. Проте це суперечить властивості монотонності дії множення натуральних чисел. Отже, наше припущення, що існують два різних числа 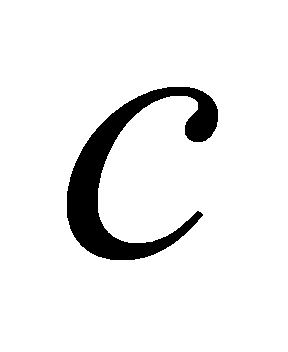 і
і 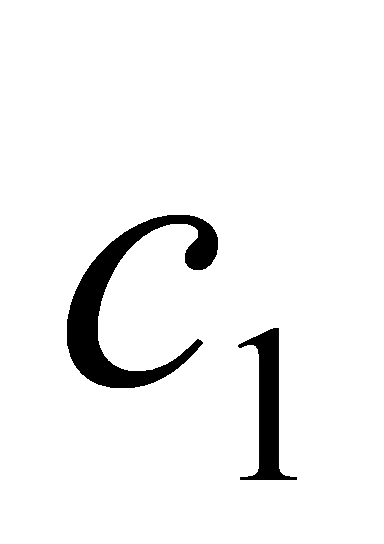 , які є частками від ділення а на b, неправильне. Теорему доведено.
, які є частками від ділення а на b, неправильне. Теорему доведено.
Із означення  випливає, що:
випливає, що:
а) частка від ділення натурального числа а на 1 дорівнює числу а, тобто  ;
;
б) частка від ділення натурального числа а самого на себе дорівнює 1, тобто 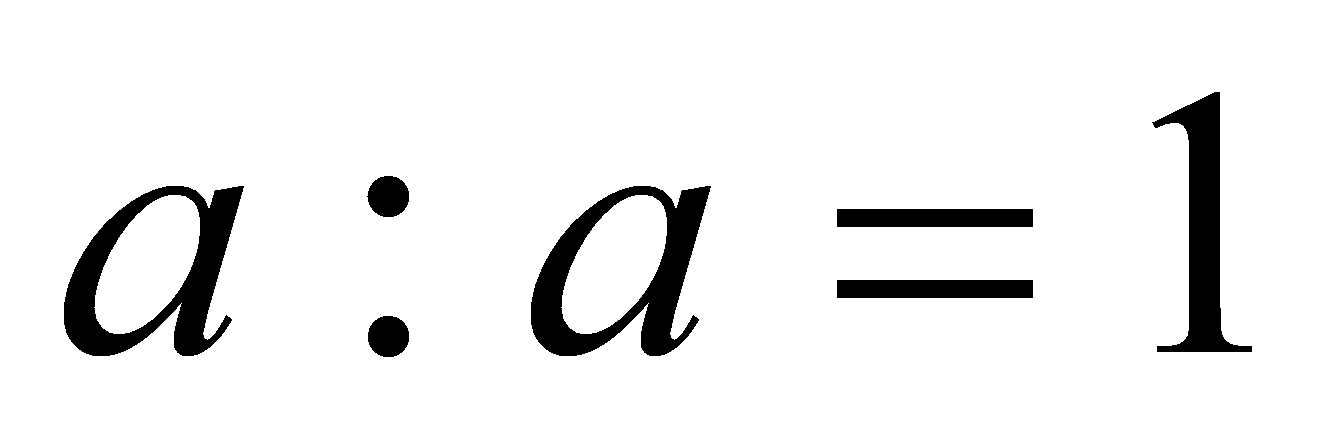 .
.
Розглянемо можливі два випадки.
1. Нехай 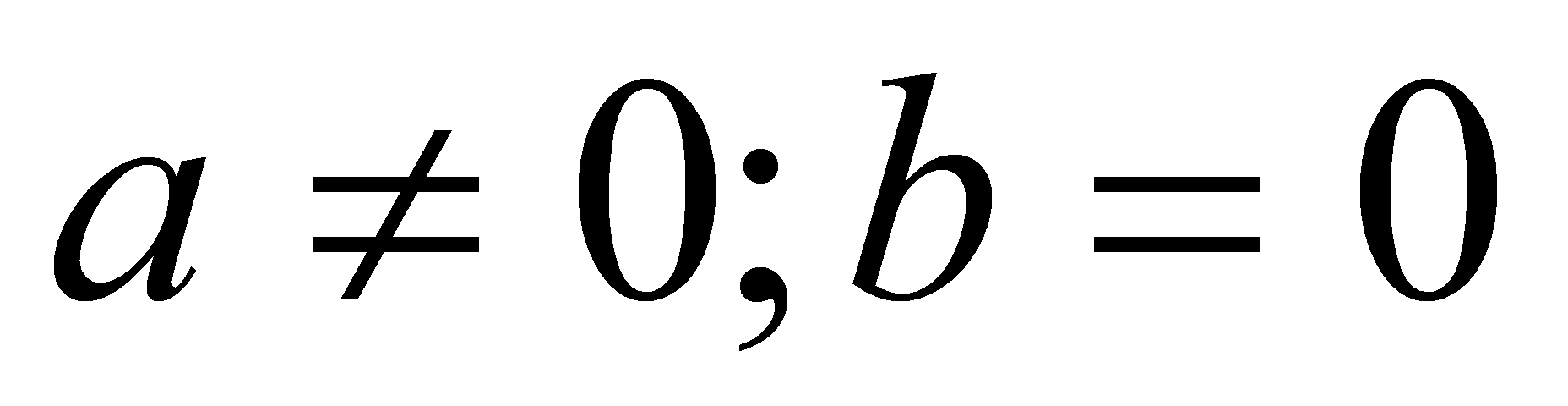 .
.
Припустимо, що частка 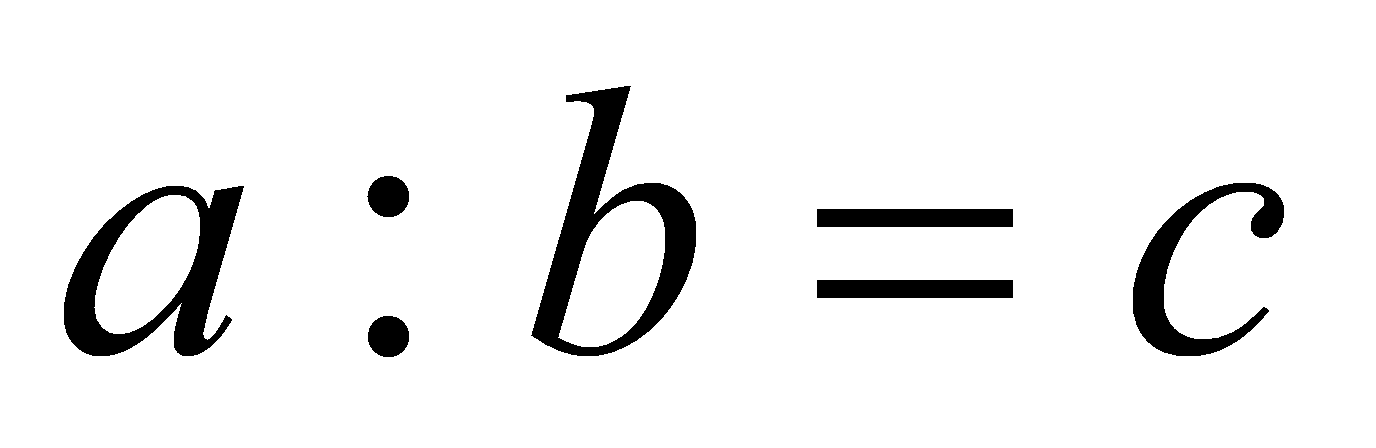 існує. За означенням частки через добуток
існує. За означенням частки через добуток  ,
, 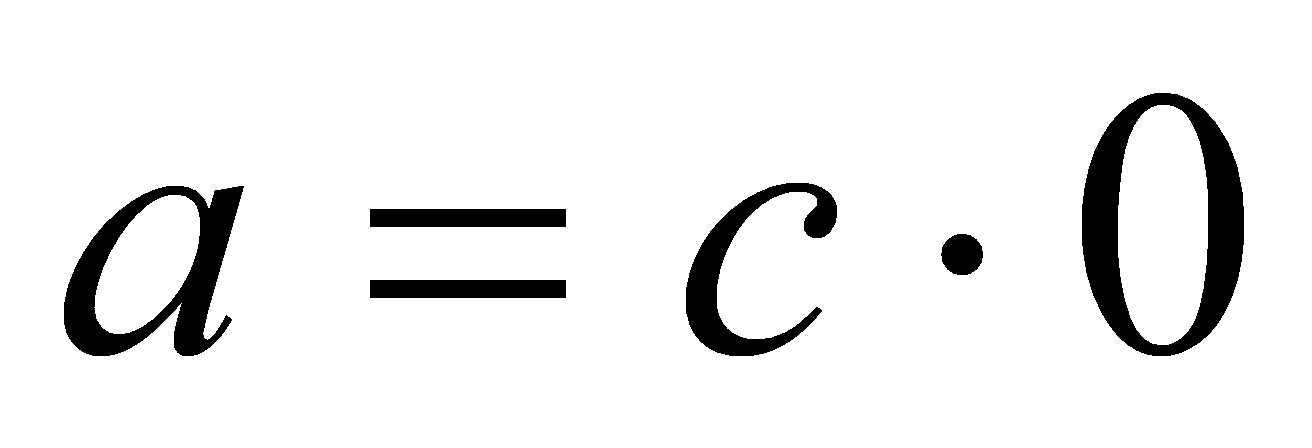 , тобто
, тобто  (за означенням добутку). Проте це суперечить умові про те, що
(за означенням добутку). Проте це суперечить умові про те, що 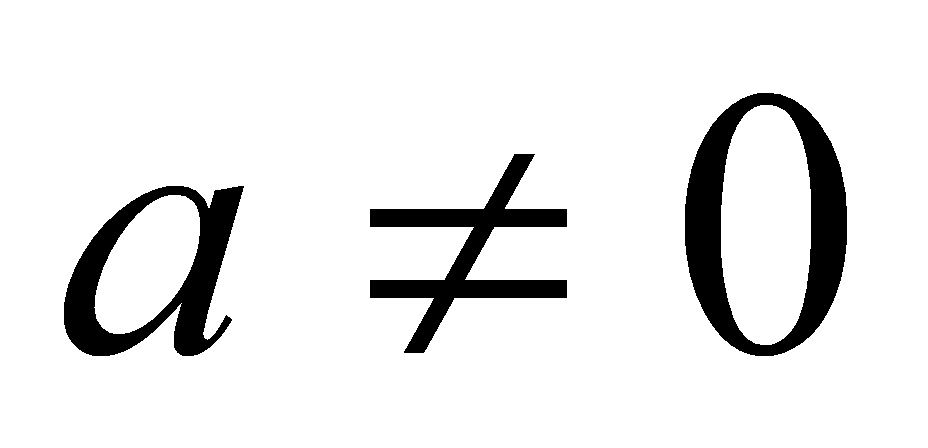 . Отже, наше припущення, що частка існує, неправильне. Тому ділення на 0 в цьому випадку неможливе.
. Отже, наше припущення, що частка існує, неправильне. Тому ділення на 0 в цьому випадку неможливе.
|
|
|
· Нехай  .
.
Припустимо, що частка 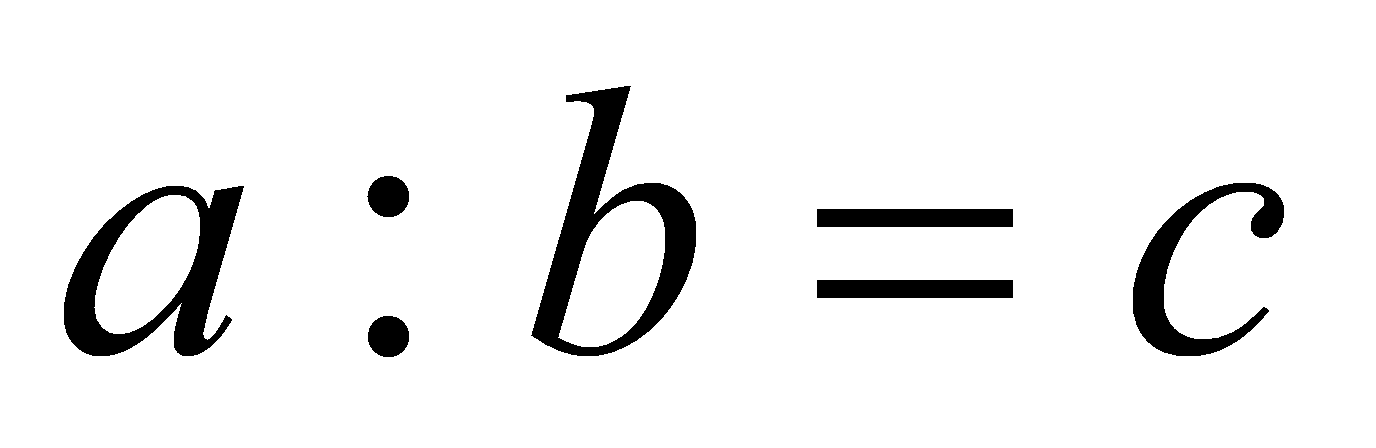 існує. За означенням частки через добуток
існує. За означенням частки через добуток  ,
, 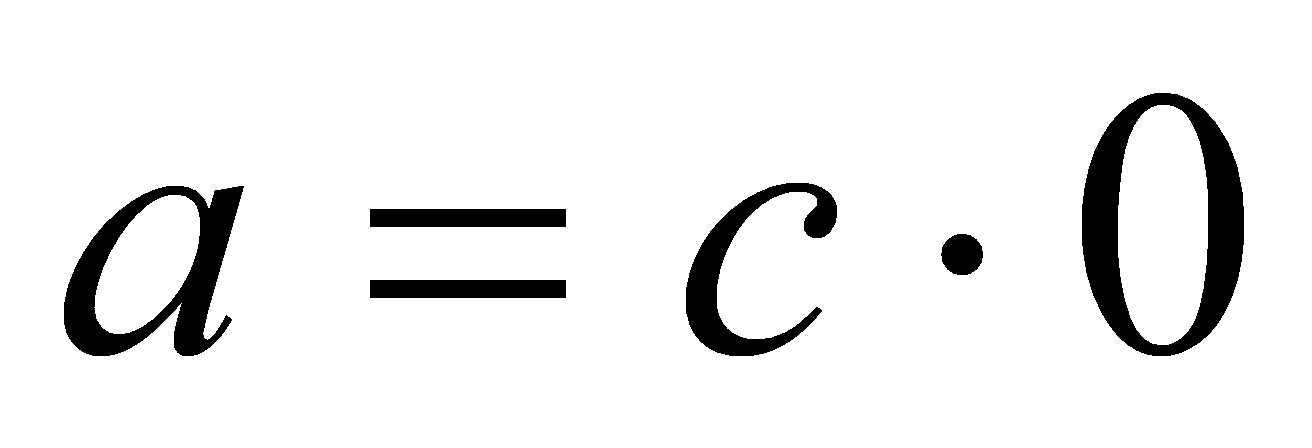 . З цього випливає, що будь-яке число с задовольняє умову
. З цього випливає, що будь-яке число с задовольняє умову 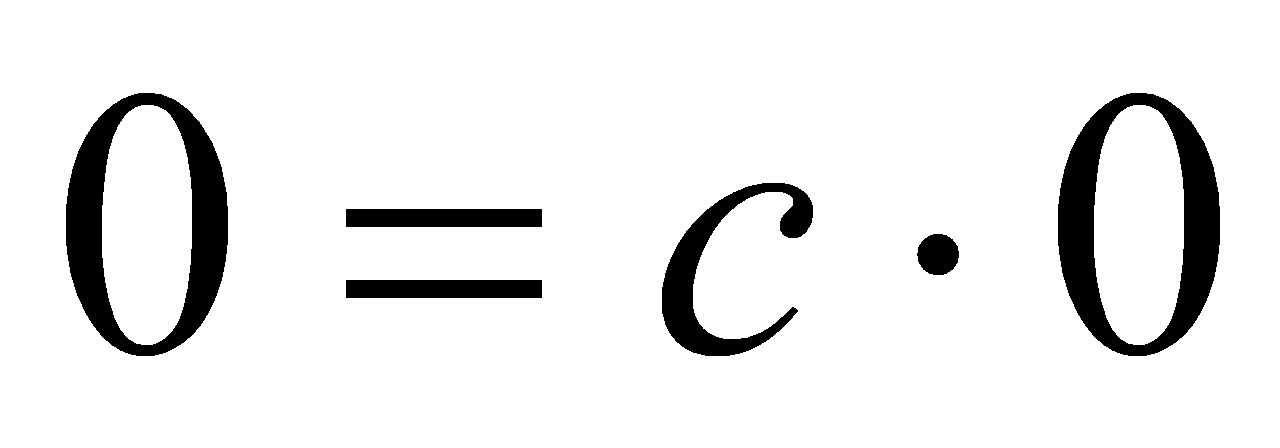 , тобто частка визначена не однозначно. Це суперечить теоремі про єдиність частки. Отже, наше припущення, що частка існує, неправильне. Тому ділення на 0 і в цьому випадку неможливе.
, тобто частка визначена не однозначно. Це суперечить теоремі про єдиність частки. Отже, наше припущення, що частка існує, неправильне. Тому ділення на 0 і в цьому випадку неможливе.
Висновок: Ділення на нуль – неможливе.
Правила ділення суми та різниці на число.
Правило ділення суми на число.
Щоб поділити суму на число, досить поділити на це число кожний доданок і добуті результати додати: 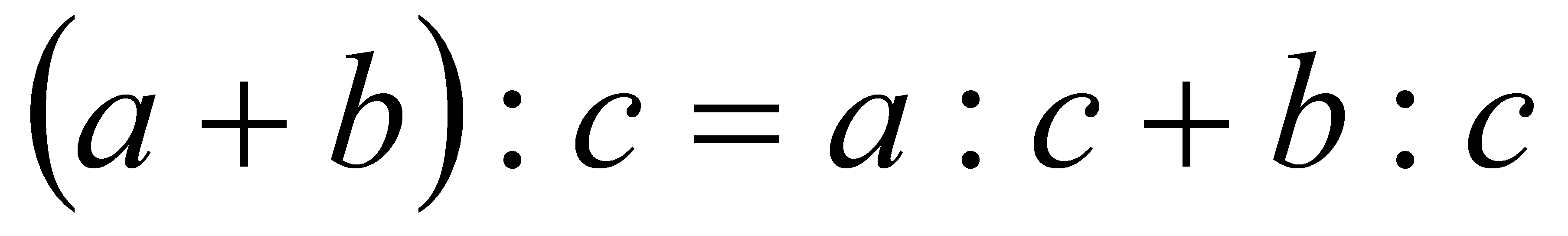 .
.
Доведення. Якщо рівність правильна, то за означенням дії ділення має бути:
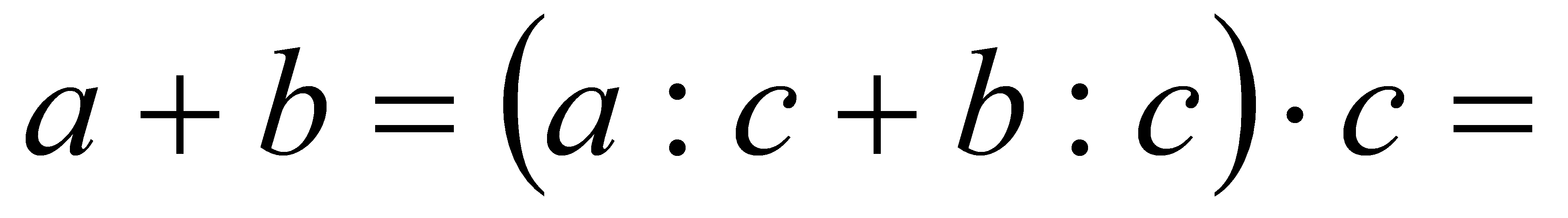 (за розподільним законом множення);
(за розподільним законом множення);
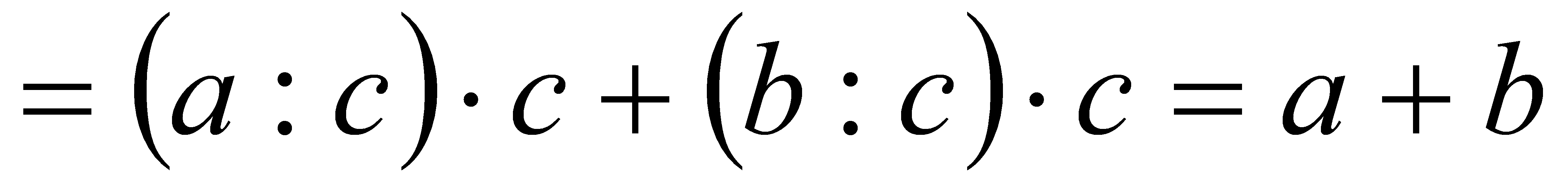 (за властивістю ділення як дії, оберненої множенню).
(за властивістю ділення як дії, оберненої множенню).
Це правило можна поширити на будь-яке число доданків:
 .
.
Правило ділення суми на число дуже важливе: воно є теоретичною основою алгоритму ділення багатоцифрових чисел.
У початкових класах його розкривають на конкретних задачах.
Задача. В одному сувої 12 м тканини, а в другому 15 м. з цієї тканини пошили плаття, витрачаючи на кожне по 3 м. Скільки платтів пошили?
|
|
|
Розв’язують задачу двома способами, дістаючи при цьому різні, але еквівалентні між собою числові формули розв’язку:
1-й спосіб 2-й спосіб


Висновок.  .
.
Дата добавления: 2019-02-13; просмотров: 764; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
