Минимальное расстояние линейного кода
Расстоянием Хэмминга между векторами x = (x1, x2, …, xn) и y = (y1, y2, …, yn) называется число d(x, y), равное количеству координат, в которых различаются эти векторы.
Свойства расстояния Хэмминга:
1. d(x, y) ≥ 0; d(x, y) = 0 ó x = y
2. d(x, y) = d(y, x)
3. d(x, y) ≤ d(x, z) + d(z, y)
Весомвектора x = (x1, x2, …, xn) называется количество ненулевых координат. Вес вектора x обозначается w(x).
Свойства веса вектора:
1. w(x) ≥ 0
2. d(x, y) = w(x–y)
3. w(x) = d(x, θ)
Пример 3. Пусть x = (010111), y = (101100), тогда d ( x , y ) = 5, w(x) = 4, w(y) = 3.
Минимальным расстояниемлинейного кода C называется минимальное из расстояний между различными кодовыми векторами. Обозначение:  .
.
Однако даже для небольшого линейного кода из примера 2 найти минимальное расстояние по определению не просто.
Теорема 1. Минимальное расстояние линейного кода равно минимальному из весов ненулевых кодовых векторов. 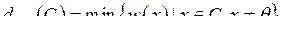 .
.
Доказательство. Множество всех кодовых векторов С с операциями сложения векторов и умножения вектора на скаляр из Fq образует линейное пространство – подпространство пространства всех n-мерных векторов над Fq. Это легко показать по критерию подпространства, учитывая, что С – это множество решений однородной системы линейных уравнений 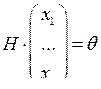 .
.
Значит, (С, +) – абелева группа, и разность двух кодовых векторов принадлежит С.
Тогда по определению  . По свойству 2 веса получим:
. По свойству 2 веса получим:  . Так как (С, +) – абелева группа, то x – yÎС. С другой стороны, любой кодовый вектор z может быть записан в виде разности двух кодовых векторов: z = z – q. Поэтому введя обозначение z = x – y, получим:
. Так как (С, +) – абелева группа, то x – yÎС. С другой стороны, любой кодовый вектор z может быть записан в виде разности двух кодовых векторов: z = z – q. Поэтому введя обозначение z = x – y, получим:
|
|
|
 , ч.т.д. □
, ч.т.д. □
В частности, для линейного кода из примера 2 веса всех ненулевых кодовых векторов равны 3, и поэтому dmin (С) = 3.
Минимальное расстояние определяет корректирующие возможности кода.
При декодировании линейных кодов используют метод декодирования в «ближайшего соседа». Изложим его суть.
Пусть при передаче кодового вектора x = (x1x2…xn)Î C получен вектор y = (y1y2…yn).
Вектор e = y – x = (y1–x1 … yn–x n) называется вектором ошибки.
Если полученный вектор у является кодовым, то считают, что ошибки не было, а если не является кодовым, то ищут ближайший к нему кодовый вектор, и считают, что именно он был передан по каналу связи.
Полученный вектор y декодируется в кодовое слово 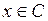 , удовлетворяющее условию, что вектор ошибки
, удовлетворяющее условию, что вектор ошибки 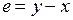 имеет минимальный вес.
имеет минимальный вес.
Таким образом, если при передаче кодового вектора x = (x1x2…xn)получен другой кодовый вектор y = (y1y2…yn), произойдёт ошибка декодирования. Поэтому, чем больше расстояние между кодовыми словами, тем больше корректирующие возможности кода.
Если структура кода позволяет исправлять до t ошибок и позволяет обнаруживать (не обязательно исправлять) до s ошибок в любых позициях любого кодового слова, то говорят, что код может исправлять t ошибок и обнаруживать s ошибок.
|
|
|
Теорема 2. Линейный код C с минимальным расстоянием dmin(C) = d может обнаруживать d–1 ошибку и исправлять 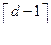 ошибок.
ошибок.
Доказательство.
I. 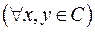 d(x, y) ≥ d (т.к. d – минимальное расстояние).
d(x, y) ≥ d (т.к. d – минимальное расстояние).
Пусть при передаче кодового вектора x = (x1x2…xn)Î C получен вектор y = (y1y2…yn). Если при передаче произошло не более d–1 ошибок, то d(x, y) ≤ d–1 < d => y не является кодовым вектором (yÏC), и это можно обнаружить, например, с помощью проверочной матрицы H: 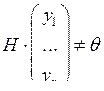 .
.
При этом  , такие что d(x, y) = d. Поэтому d ошибок, переводящие кодовый вектор x в другой кодовый вектор y, не будут обнаружены.
, такие что d(x, y) = d. Поэтому d ошибок, переводящие кодовый вектор x в другой кодовый вектор y, не будут обнаружены.
II. Шаром радиуса r с центром в векторе x = (x1x2…xn) называется множество векторов расстояние от которых до x не превосходит r.
Sr ( x ) = { y = (y1y2…yn) | d ( x , y ) ≤ r}.
Например, S1(001) ={001, 101, 011, 000}.
Опишем вокруг каждого кодового вектора x шар радиуса t. В этом шаре находятся все векторы, получаемые из x в случае, если произошло не более t ошибок. Если код исправляет t ошибок, то все эти векторы декодируются в x, и шары радиуса t с центром в различных кодовых словах не пересекаются, - иначе возникнет проблема декодирования векторов, попавших в пересечение. Рассмотрим два ближайших кодовых вектора x 1, x 2ÎC, такие что d(x 1, x 2) = d.
|
|
|

Из рисунка видно, что для того, чтобы шары не пересекались, должно выполняться условие: 2t < d, откуда имеем 2t £ d–1 и
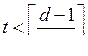 .□
.□
В частности, линейный код из примера 2, как и любой другой код с мимнимальным расстоянием 3, может обнаруживать 3-1=2 ошибки, и исправлять 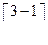 =1 ошибку.
=1 ошибку.
Декодирование линейных кодов
Опишем теперь простой алгоритм декодирования для линейных кодов. Рассмотрим линейный (n, k) – код С над Fq как подпространство в Fqn. Фактопространство Fqn/С состоит из всех смежных классов а + С = { a + x 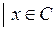 } для аÎ Fqn. Каждый смежный класс содержит qk векторов. Имеем разбиение пространства Fqn :
} для аÎ Fqn. Каждый смежный класс содержит qk векторов. Имеем разбиение пространства Fqn :
Fqn = С  ( а(1) + С )
( а(1) + С )  ….
…. 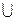 ( а(t) + C), t = qn-k – 1.
( а(t) + C), t = qn-k – 1.
Если декодером получен вектор у, то у должен лежать в одном из этих смежных классов, скажем в аi + С. Если передавалось кодовое слово х, то для вектора ошибок е имеем е = у – хÎ аi + С – х = аi + С. Поэтому если получен вектору, то возможные векторы ошибок е лежат в смежном классе, содержащем у. Наиболее правдоподобной ошибкой служит вектор е минимального веса в смежном классе вектора у. Поэтому у декодируется в кодовое слово x = у – e.
Вектор минимального веса в смежном классе называется лидером смежного класса. Если таких векторов несколько, то один из них произвольно выбирается в качестве лидера. Пусть а(1), …….,а(t) – лидеры смежных классов, отличных от С. Сначала расположим все векторы из Fnq в виде следующей таблицы (предложенной Слепяном):
|
|
|
х = 0 x2 ……x(qk) 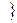 - кодовые слова
- кодовые слова
a(1) = x(1) a(1) + x(2) …..a(1) + x(qk)
…………………………………… остальные смежные
a(t) + x(1) a(t) +x(2) …...a(t) + x(qk) классы
Если получен вектор у, то нужно отыскать его в таблице. Пусть у = а + х; тогда декодер решает, что ошибка e есть лидер смежного класса а. Поэтому у декодируется в кодовое слово х = у - e. Кодовое слово х является первым элементом столбца, содержащего у. Смежный класс вектора у может быть найден с помощью вычисления так называемого синдрома.
Пусть Н – проверочная матрица линейного (n , k) – кода С. Тогда вектор S (у)= Ну T длины n - k называется синдромом вектора у.
Свойства синдрома:
1) S(y) = 0  y
y 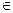 C.
C.
2) S(y(1)) = S(y(2))  y(1) + C = y(2) + C
y(1) + C = y(2) + C
Доказательство.
1) Утверждение следует из определения линейного кода.
2) S(y(1)) = S(y(2))  Ну(1)Т = Ну(2)Т
Ну(1)Т = Ну(2)Т  Н(у(1)- у(2))Т = 0
Н(у(1)- у(2))Т = 0 
 у(1)- у(2)
у(1)- у(2) 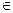 С
С  у(1) +С = у(2) + С.
у(1) +С = у(2) + С.
Таким образом, смежные классы определяются синдромами их векторов. Если е = у – х, где х 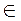 С,
С,
у 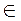 Fnq,то S(y) = S(x+e) = S (x) + S (e) = S(e),
Fnq,то S(y) = S(x+e) = S (x) + S (e) = S(e),
т.е. у и е лежат в одном смежном классе. Можно дать иную формулировку алгоритма декодирования:
Сформулируем алгоритм синдромного декодирования.
Пусть получен вектор у 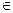 Fqn.
Fqn.
Шаг 1: вычисляем S (у). Если S (у)= q, то ошибок не произошло. Иначе переходим к шагу 2.
Шаг 2: находим лидер смежного класса e с синдромом S ( e )= S (у).
Шаг 3: исправляем ошибку. y – e = x – переданный кодовый вектор.
Пример:
Пусть С – бинарный линейный (4,2) – код с порождающей матрицей G и проверочной матрицей Н, где
G = 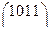 , Н =
, Н =  :
:
Составим таблицу смежных классов (её называют также таблицей Слепяна):
сообщения 00 10 01 11
кодовые слова 0000 1011 0101 1110 (00)Т
другие 1000 0011 1101 0110 (11)Т
смежные 0100 1111 0001 1010 (01)Т
классы 0010 1001 0111 1100 (10)Т
лидеры синдромы
смежных
классов
Первый способ: декодирование по таблице. Если получен вектор у = 1111, то ищем его в таблице, и заменяем на кодовое слово х= 1011, которое является первым элементом столбца, содержащего у. Соответствующим сообщением будет 10.
Второй способ: синдромное декодирование. Если получен вектор у = 1111, то ищем S(y) = HyT =  = (01)T. Поэтому ошибка e = 0100 и у декодируется снова в x = у - e = 1011. При таком способе исправления ошибок вся таблица не нужна, достаточно оставить первый столбец – столбец лидеров (они будет векторами ошибок), и последний столбец – столбец соответствующих лидерам синдромов.
= (01)T. Поэтому ошибка e = 0100 и у декодируется снова в x = у - e = 1011. При таком способе исправления ошибок вся таблица не нужна, достаточно оставить первый столбец – столбец лидеров (они будет векторами ошибок), и последний столбец – столбец соответствующих лидерам синдромов.
Для больших линейных кодов использование лидеров смежных классов практически невозможно. Например, (50,20) – код над F2 имеет более 109 смежных классов. Поэтому требуется конструировать специальные коды, наподобие определяемых ниже кодов Хэмминга. Отметим, что в бинарном случае синдром легко интерпретируется. Так как S(y) = НеТ для у = х + е, у Î F 2 n, xÎC, мы имеем следующий факт.
Теорема 3. Для бинарного кода синдром полученного вектора равен сумме столбцов проверочной матрицы Н, соответствующих тем координатам, в которых появились ошибки.
Дата добавления: 2019-02-12; просмотров: 1285; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
