Упорядоченное движение частиц грубодисперсных аэрозолей

(метод траекторий)

Поведение газодисперсных систем во многом определяется динамикой движения одиночных частиц, которая, в свою очередь, существенно зависит от их размеров. Относительно крупные частицы (d > 20 мкм) слабо реагируют на турбулентные пульсации несущего газа и уравнение их движения аналогично уравнению движения отдельно взятой частицы в вязкой ламинарной среде :

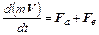(2.36)

где 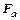- сила аэродинамического взаимодействия, 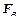- равнодействующая сторонних (внешних) сил, действующих на частицу. К ним относятся сила тяжести, электрические, магнитные и другие силы. Взаимодействие частиц с потоком газа носит очень сложный характер , однако, в большинстве практически важных случаев с достаточной для инженерной практики точностью его можно свести к силе сопротивления среды, которая для сферических частиц имеет вид :

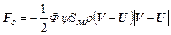(2.37)

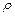- коэффициент аэродинамического сопротивления шара; S _м – площадь миделевого сечения частицы; - плотность газа; U,V - векторы скорости частицы и газа. Ф – динамический коэффициент формы частицы.

Форма частицы	Динамический коэффициент, Ф
Сферическая	1
Округлая	1.83
Угловатая	2.48
Продолговатая	3.18
Пластинчатая	6.5

Величина коэффициента аэродинамического сопротивления шара существенно зависит от режима его обтекания, который характеризуется числом Рейнольдса:

(2.38)

В следующей таблице приведены выражения для коэффициента 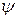в различных диапазонах чисел Рейнольдса.

	Область применения	Автор
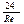
	Re <0.2	Стокс
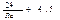
	Re <1	Озеен
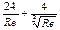
	1<Re<10³	Клячко

Если сила, действующая со стороны воздуха на частицу, выражается формулой Стокса

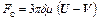(2.39)

то уравнение движения частицы может быть записано так:

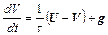(2.40)

где - время релаксации частицы.

Для частиц размером 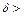10 мкм силу аэродинамического взаимодействия необходимо вычислять по формуле Клячко. При этом уравнение движения примет вид:

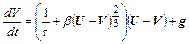
(2.41)

где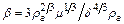

Пример. Рассмотрим задачу о падении сферической частицы в неподвижном воздухе.

Проектируя уравнение движения частицы на направление силы тяжести, получим линейное уравнение первого порядка:

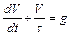(2.42)

решение которого при начальном условии 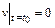имеет вид:

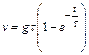(2.43)

Из последней формулы следует, что скорость частицы асимптотически приближается к постоянной величине: 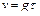, называемой седиментационной скоростью.

Практически седиментационная скорость достигается очень быстро. Так, за время 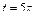величина скорости частицы v достигает значения . Найдем область применимости формулы .

Из условия стоксовского режима обтекания Re < 0.2 получим:

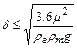(2.44)

Для пылей строительных материалов с плотностью 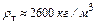формула справедлива для частиц размеро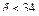м мкм.

Седиментационная скорость более крупных частиц должна определяться с помощью уравнения 2.41.

Проектируя это уравнение на направление силы тяжести, получим:

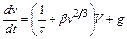(2.45)

Данное уравнение может быть решено только численно с помощью ЭВМ.

Если не интересоваться динамикой установления скорости оседания частицы, а определять только ее величину, то вместо дифференциального уравнения можно рассмотреть алгебраическое уравнение, которое получается из 2.45, если положить в нем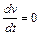

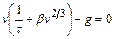(2.46)

Уравнение 2.45 может быть решено одним из численных методов.

В пристенных областях, где имеют место значительные градиенты скорости газа, необходимо учитывать турбулентные пульсации скорости несущей среды, приводящие к возникновению специфических форм движения частиц - их подъемный и турбулентной миграции.

Причиной этих движений являются сила Магнуса

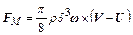, (2.47)

связанная с собственным вращением частиц с угловой скоростью , возникающим в результате соударений частиц с твердыми поверхностями, а также сила Сафмена

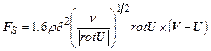, (2.48)

связанная с вращением частиц из-за градиента скорости газа в сдвиговых потоках.

Коэффициент аэродинамического сопротивления, как известно, является функцией числа Рейнольдса. В стоксовской области ( 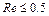) будем использовать зависимость:

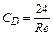
а для переходного режима обтекания ограничимся уточненным вариантом эмпирической формулы Клячко:

(2.49)

которая с удовлетворительной точностью также охватывает и стоксовскую область. Здесь .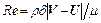

Уравнение движения для частиц несферической формы можно переписать в виде:

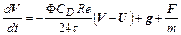(2.50)

Траектории движения частиц аэрозоля можно найти путем численного интегрирования уравнений движения (2.50) совместно с уравнениями

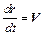(2.51)

с учетом начальных условий:

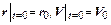(2.52)

Предварительно уравнения и начальные условия приводят к безразмерному виду, используя в качестве масштабов характерные для данного процесса размер l и скорость U₀.

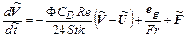(2.53)

где 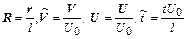- безразмерные радиус-вектор, скорость частицы и газа, а также безразмерное время; 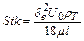- число Стокса, - число Фруда, 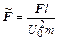- безразмерная внешняя сила, 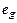- единичный вектор ускорения силы тяжести. Дальше обозначение безразмерности величины "~" будем опускать.

В общем случае уравнения (2.53) могут быть решены только численно, например, методом Рунге-Кутта.

Исследование движения одиночных частиц (метод траекторий) применяется для оценки эффективности их осаждения при обтекании тел-препятствий, а также при изучении процессов вакуумной пылеуборки и пневмотранспортирования дисперсных материалов. Важным примером упорядоченного движения частиц является их гравитационное осаждение.

Выведем теперь уравнение движения коагулирующих частиц [180]. Поскольку масса частиц в процессе коагуляции непрерывно возрастает, то уравнение их движения следует записать так:

(2.54)

Предположим, что форма частиц в результате их коагуляции не меняется, т.е. укрупнение частиц носит автомодельный характер. Тогда коэффициенты К_М и К_D будут сохранять свои значения, а уравнение (2.118) с помощью соотношения

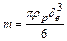
и уравнения (2.54) можно привести к виду:

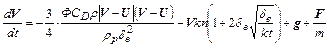(2.55)

Система обезразмеренных уравнений, описывающая движение коагулирующих частиц, может быть записана так:

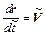
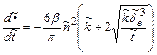(2.56)

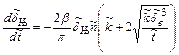
Здесь в качестве базисных для обезразмеривания величин выбраны начальный эквивалентный размер частиц d₀, их начальная счетная концентрация n₀, характерная скорость газового потока U₀и характерный размер l. Тогда:

(2.57)

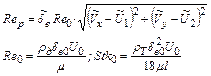(2.58)

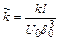- безразмерный коэффициент коагуляции;

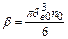- объемная концентрация дисперсной фазы.

Из рассмотренных уравнений следует, что процессы упорядоченного движения частиц и их коагуляции взаимосвязаны: изменение размеров и массы частиц непосредственно влияют на их аэродинамические свойства и динамику; с другой стороны, движение частиц определяет продолжительность пребывание частиц в зоне коагуляции, а значит и степень их укрупнения.

Важное практическое значение имеет моделирование движения и коагуляции частиц аэрозоля в сильных электрических полях.

При записи этой системы уравнений будем исходить из следующих основных физических предпосылок:

1. Полный заряд частиц равен сумме зарядов, рассчитанных по уравнениям ударной и диффузионной зарядки;

2. Влияние объемного заряда, создаваемого частицами, а также поперечного движения газа (электрический ветер) не учитывается;

3. Подвижность ионов в межэлектродном пространстве считается постоянной;

4. Электрический заряд частиц несферической формы равен заряду сферических частиц эквивалентного размера.

Система уравнений, описывающая в естественных переменных движение, зарядку и коагуляцию частиц аэрозоля в поле коронного разряда имеет вид:

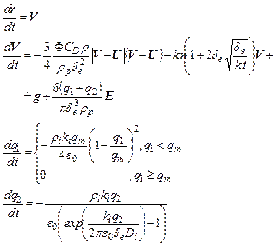(2.59)

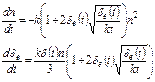(2.60)

Первые два уравнения этой системы описывают движение заряженной частицы переменной массы в потоке газа под действием электрической и гравитационной сил. Два следующих уравнения определяют ударный и диффузионный механизмы зарядки частиц. Два последних уравнения описывают изменение счетной концентрации и эквивалентного размера частиц. При этом предполагается, что форма частиц в результате коагуляции в общих чертах сохраняется (для капельных аэрозолей это утверждение выполняется точно).

В уравнениях (2.59) приняты следующие обозначения: q ₁, q ₂ - ударная и диффузионная составляющие заряда частицы, q_m - максимальное значение ударной составляющей заряда частицы, определяемое формулой Потенье :

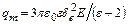(2.61)

e₀, e - диэлектрическая проницаемость вакуума и вещества частицы (для пылей строительных материалов e » 4), r_i - плотность объемного заряда ионов, e - заряд электрона (e = 1.6×10^-19 Кл), k_i - подвижность ионов, n_i, n - счетная концентрация ионов и частиц аэрозоля.

Дифференциальные уравнения дополним следующими начальными условиями:

Дата добавления: 2019-02-12; просмотров: 237; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒

Мы поможем в написании ваших работ!