Дифференциальное уравнение относительного движения точки
Иногда при решении задач бывает удобно рассматривать движение точки по отношению к подвижной системе отсчета. Если точка совершает сложное движение, то по теореме о сложении ускорений абсолютное ускорение есть геометрическая сумма переносного, относительного и кориолисова ускорения, т.е.
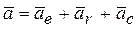. (2)
Подставив (2) в (1), получим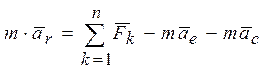 
(3)
Обозначим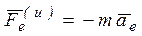 
, 
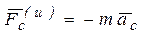. Тогда формула (3) с учетом обозначений примет вид 
.
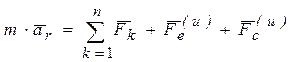Это и есть дифференциальное уравнение относительного движения точки. дифференциальное уравнение относительного движения точки ни чем не отличается от основного уравнения динамики, если к силам, действующим на точку, добавить переносную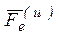 
и Кориолисову 
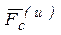силы инерции. Если переносное движение является поступательным, прямолинейным и равномерным, то 
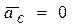и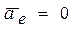 
. В этом случае дифференциальное уравнение относительного движения будет совпадать с основным уравнением динамики. Это говорит о том, что система отсчёта, двигающаяся относительно неподвижной поступательно, равномерно и прямолинейно, является инерциальной.
Свободные колебания
Свободными называются колебания точки, происходящие под действием только восстанавливающей силы. Сила называется восстанавливающей, если она все время стремится вернуть точку в положение равновесия. Примером восстанавливающей силы является сила упругости пружины. Если восстанавливающая сила пропорциональна смещению точки из положения равновесия, то она называется линейной восстанавливающей силой.
|
|
|
Пусть на точку М массой m действует линейная восстанавливающая сила упругости (рис. 2): Fупр = сΔ, где с – жесткость пружины (физический смысл жесткости - это сила, необходимая для деформации пружины на единицу длины), в Н/м; Δ – деформация пружины, м.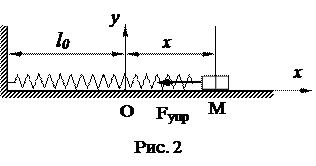 
На рис. 2 l 0 – длина недеформированной пружины. Выбрав начало координат в положении равновесия – т. О, запишем основное уравнение динамики в проекции на ось x: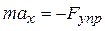 
, или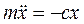 
.
Отсюда получим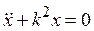 
(4)
Выражение (4) – это и есть уравнение свободных колебаний точки. Здесь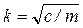 
называется круговой частотой колебаний (физический смысл: число колебаний за 2π секунд), с-1. Общее решение дифференциального уравнения (4) имеет вид:
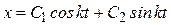. (5)
Взяв производную по времени, имеем
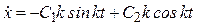. (6)
Постоянные интегрирования С1 и С2 найдем из начальных условий:
|
|
|
при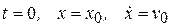 
. (7)
Подставив (7) в (5) и (6), находим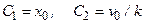 
.
С учетом этого решение (5) принимает вид:
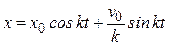. (8)
Решение (8) можно записать в виде:
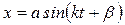, (9)
где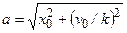 
- амплитуда колебаний, м; 
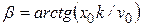- начальная фаза колебаний, рад.
Из (9) видно, что свободные колебания являются гармоническими. Период колебаний можно найти по формуле:
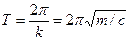. (10)
Влияние постоянной силы на свободные колебания
Пусть, кроме силы упругости, на точку действует некоторая постоянная сила F (рис. 3). В этом случае основное уравнение динамики примет вид:
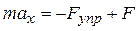. (11)
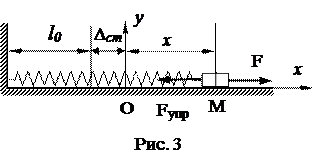Выбрав начало координат в положении равновесия – т. О, имеем: 
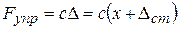, где Δст – статическая деформация пружины под действием силы F.
|
|
|
С учетом этого уравнение (11) примет вид: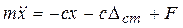 
. Но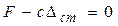 
, тогда получим 
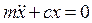или
, (12)
где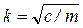 
.
Сравнивая уравнения (4) и (12) видим, что они совпадают. Следовательно, совпадают и их решения. Таким образом, постоянная сила не изменяет характер колебаний точки, она лишь смещает центр колебаний в направлении действия силы на расстояние, равное статической деформации пружины.
По формуле (10):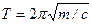 
, учитывая, что 
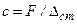, имеем 
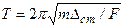. Если постоянная сила является силой тяжести, то 
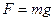и период колебаний можно найти по формуле: 
.
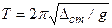Дата добавления: 2019-02-12; просмотров: 212; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!