Средние коэффициенты эластичности

Средние коэффициенты эластичности для линейного уравнения множественной регрессии рассчитываются по формуле:

Они показывают, на сколько процентов в среднем по совокупности изменится результат у от своей величины при изменении фактора на 1% от своего значения при неизменных значениях других факторов.

Сделайте заготовку таблицы для вычислений (см. рисунок).

С помощью встроенной функции найдите в ячейке М21 среднее значение результативного признака Y (диапазон ячеек В2:В30).
В ячейке М22 найдите среднее значение факторного признака Х1 (диапазон ячеек С2:С30).
В ячейке М23 найдите среднее значение факторного признака Х2 (диапазон ячеек D2:D30).
В ячейку М24 введите формулу: =M11*M22/M21 (находим коэффициент эластичности по формуле).
В ячейку М25 введите формулу: =M12*M23/M21 (находим ).
Вы должны получить следующие результаты:

Вывод:

1. С изменением затрат на модернизацию производства (фактор Х1) на 1% прирост прибыли изменится на 0,33% при условии, что затраты на рекламу (фактор Х2) останутся на прежнем уровне.

2. С изменением затрат на рекламу (фактор Х2) на 1% прирост прибыли изменится всего на 0,001% при условии, что затраты на модернизацию производства (фактор Х1) останутся на прежнем уровне.

Показатели тесноты связи

Индекс множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.

, где

- остаточная дисперсия для уравнения 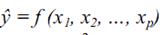, которая вычисляется по формуле:

Индекс множественной корреляции для уравнения множественной регрессии в стандартизированном виде определяется по формуле:

При линейной зависимости коэффициент множественной корреляции можно определить по формуле:

, где

- определитель матрицы парных коэффициентов корреляции,

- определитель матрицы межфакторной корреляции.

Качество построенной модели оценивают с помощью коэффициента множественной детерминации, который рассчитывается как квадрат индекса множественной корреляции:

Скорректированный индекс детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:

, где

n – число наблюдений, m – число факторов.

I способ.

Найдём индекс множественной корреляции по формуле:

1. В книге MS Excel перейдите на новый лист и скопируйте на него данные с первого листа из диапазона А1:D30 (исходные данные для результативного признака Y и факторных признаков X1 и Х2).

2. Сделайте заготовки таблиц для вычислений (см. рисунок).

3. Найдём теоретические значения результативного признака Y с помощью полученного уравнения множественной регрессии 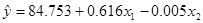. В ячейку Е2 введите формулу:

=Лист1!$M$10+Лист1!$M$11*Лист2!C2+Лист1!$M$12*Лист2!D2 (в эту формулу мы подставляем вычисленные значения коэффициентов а, b1 и b2, находящиеся на Листе 1. Скопируйте эту формулу вниз в диапазон ячеек Е3:Е30).

4. В ячейку F2 введите формулу: =(B2-E2)^2. Скопируйте эту формулу вниз в диапазон ячеек F3:F30.

5. В ячейке I2 найдём величину 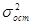. Введите в ячейку I2 формулу: =СУММ(F2:F30)/29.

6. В ячейке I3 найдём величину . Квадрат среднего квадратического отклонения – это дисперсия. Нам требуется найти дисперсию результативного признака Y (данные, находящиеся в диапазоне ячеек В2:В30). Для вычисления дисперсии используем встроенную функцию MS Excel. Введите в ячейку I3 формулу: =ДИСПР(B2:B30).

7. Вычислим индекс множественной корреляции. Введите в ячейку I5 формулу: =КОРЕНЬ(1-I2/I3).

8. Вы должны получить следующие результаты:

II способ

Найдём индекс множественной корреляции по формуле:

Для этого будем использовать уравнение регрессии в стандартизированном виде:

1. Создайте заготовку таблицы для вычислений (см. рисунок).

2. С помощью встроенной функции КОРРЕЛ ( ) вычислите в ячейке I7 линейный коэффициент корреляции для результативного признака Y и факторного признака X1.

3. В ячейке I8 вычислите линейный коэффициент корреляции для результативного признака Y и факторного признака Х2.

4. В ячейке I9 и I10 скопируйте значения стандартизированный коэффициентов и с Листа 1.

5. Вычислим индекс множественной корреляции по имеющейся формуле. Установите курсор в ячейку I12 и введите формулу: =КОРЕНЬ(I7*I9+I8*I10).

6. Вы должны получить следующие результаты:

III способ

Найдём коэффициент множественной корреляции, используя формулу, выведенную специально для уравнения множественной регрессии линейного вида:

Для нашего случая (один результативный признак и два факторных) имеем:

- определитель матрицы парных коэффициентов корреляции.

- определитель матрицы межфакторной корреляции.

1. Составим матрицу коэффициентов парной корреляции. Вызовите пункт меню Сервис/Анализ данных… В открывшемся диалоговом окне выберите пункт Корреляция. В новом открывшемся диалоговом окне установите следующие параметры: входной интервал – В2:D30, группирование – по столбцам, выходной интервал – К2. Нажмите Ок.

2. Вы должны получить следующий результат:

3. Оформите эту таблицу и дополните пустые ячейки нужными данными (см. рисунок).

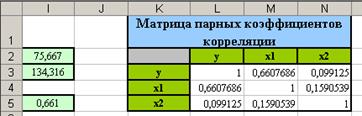
4. Построим матрицу межфакторной корреляции. Вызовите пункт меню Сервис/Анализ данных… В открывшемся диалоговом окне выберите пункт Корреляция. В новом открывшемся диалоговом окне установите следующие параметры: входной интервал – С2:D30, группирование – по столбцам, выходной интервал – К8. Нажмите Ок.

5. Вы должны получить следующий результат:

6. Оформите эту таблицу и дополните пустые ячейки нужными данными (см. рисунок).

7. Вычислим определители матриц и коэффициент корреляции.

a. Создайте заготовку таблицы для вычислений (см. рисунок).

b. В ячейке L12 вычислите определитель матрицы парных коэффициентов корреляции (диапазон ячеек L3:N5) с помощью встроенной функции МОПРЕД ( ). Не забывайте при использовании этой функции нажимать комбинацию клавиш Ctrl, Shift и Enter.

c. Аналогичным образом в ячейке L13 вычислите определитель матрицы межфакторной корреляции (диапазон ячеек L9:M10).

d. Вычислим коэффициент корреляции по имеющейся формуле. Установите курсор в ячейку L15 и введите формулу: =КОРЕНЬ(1-L12/L13).

e. Вы должны получить следующие результаты:

Индекс детерминации

Индекс детерминации – это квадрат коэффициента корреляции.

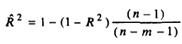, где n – число наблюдений, m – число факторов.

1. Создайте заготовку таблицы для вычислений (см. рисунок).

2. В ячейке I17 вычислите квадрат коэффициента корреляции, используя значения находящееся в ячейке I12.

3. В ячейке I18 вычислим скорректированный коэффициент детерминации по имеющейся формуле. Установите курсор в ячейку I18 и введите формулу: =1-(1-I12^2)*(I14-1)/(I14-I15-1).

4. Вы должны получить следующие результаты:

Общий вывод:

1. Множественный коэффициент корреляции равен 0.661, следовательно, между результативным и факторным признаком присутствует прямая зависимость средней силы.

2. Из матрицы парных коэффициентов корреляции мы видим, что 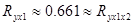, при этом между признаками Y и Х2 связь очень слабая: . Отсюда можно предположить, что изменение значения признака Х2 практически не влияет на изменении признака Y. Это предположение подтверждает и значение соответствующего среднего коэффициента эластичности: . Таким образом, изменения значения факторного признака Х1 на 1% вызовет изменения значения результативного признака Y всего на 0,001%. Следовательно, в основном на изменение значений результативного признака влияет факторный признак Х1: , то есть изменение значения факторного признака Х2 на 1% вызовет изменение значения результативного признака на 0,33%.

3. Скорректированный коэффициент детерминации равен 0,393. Это означает, что уравнение регрессии объясняет лишь 39,3% дисперсии результативного признака Y.

Дата добавления: 2019-02-12; просмотров: 190; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 Следующая ⇒

Мы поможем в написании ваших работ!