Переходные режимы от сильного поля к слабому
Из уравнений (2.3.1–2.3.4) или (2.3.6–2.3.8) следуют уравнения, описывающие эти участки; для первого
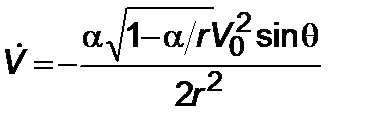 , (5.2.1)
, (5.2.1)
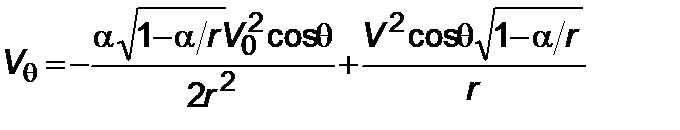 , (5.2.2)
, (5.2.2)
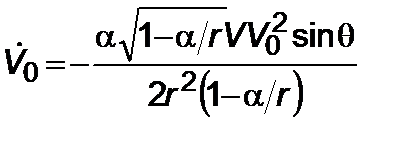 , (5.2.3)
, (5.2.3)
для второго
 ,
, 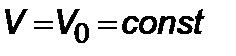 , (5.2.4)
, (5.2.4)
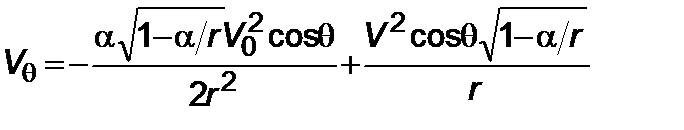 , (5.2.5)
, (5.2.5)
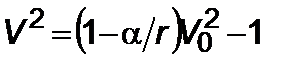 ,
, 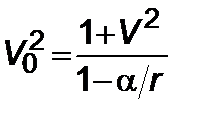 , (5.2.6)
, (5.2.6)
для 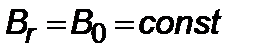 ; или
; или
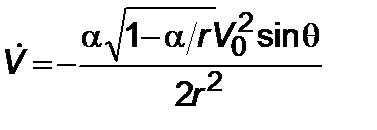 , (5.2.7)
, (5.2.7)
 , (5.2.8)
, (5.2.8)
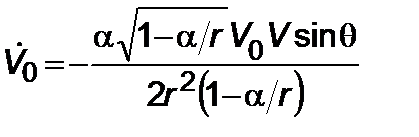 , (5.2.9)
, (5.2.9)
для 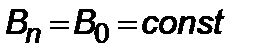 ; для третьего участка имеем
; для третьего участка имеем
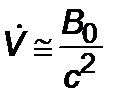 , (5.2.10)
, (5.2.10)
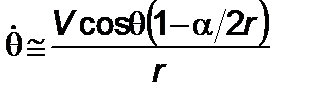 , (5.2.11)
, (5.2.11)
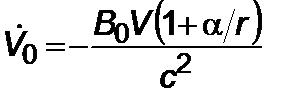 . (5.2.12)
. (5.2.12)
Сшивая решения по граничным зонам значениями  и
и 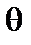 , можно построить линейные зависимости
, можно построить линейные зависимости 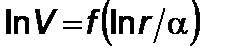
Следует заметить, что деление на указанные участки, возможно, должно быть скорректировано при условии допустимых напряжений, действующих со стороны гравитационного поля “дыры” на ракету как на протяженное тело. Данный вопрос нами не изучается.
Рис.4. Зоны деления гравитационных и реактивных сил
Особенности оптимального выведения ракеты в поле Шварцшильда
Покажем на основе ряда допущений качественные особенности функции 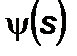 угла тангажа при выведении ракеты, не приводя подробных расчетов. Рассмотрим уравнения (2.3.6) и (2.3.7). Для простоты заменим решение (2.3.8) интегралом энергии в поле Шварцшильда, пренебрегая энергией реактивного поля
угла тангажа при выведении ракеты, не приводя подробных расчетов. Рассмотрим уравнения (2.3.6) и (2.3.7). Для простоты заменим решение (2.3.8) интегралом энергии в поле Шварцшильда, пренебрегая энергией реактивного поля
|
|
|
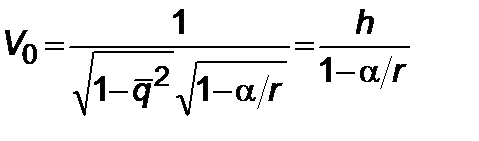 , (5.3.1)
, (5.3.1)
где 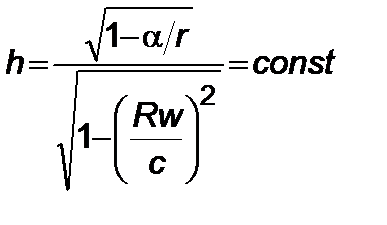 ,
, 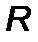 – радиус начальной круговой орбиты выведения,
– радиус начальной круговой орбиты выведения,  – угловая скорость ракеты на ней. Обозначим
– угловая скорость ракеты на ней. Обозначим  ,
, 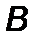 – реактивное ускорение, для упрощения считаем
– реактивное ускорение, для упрощения считаем  , что оно действует по касательной к траектории, а угол тангажа
, что оно действует по касательной к траектории, а угол тангажа 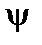 совпадает с углом
совпадает с углом 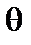 :
: 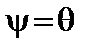 . Далее, обозначим
. Далее, обозначим 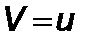 ,
, 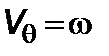 ,
, 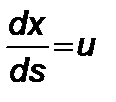 ,
, 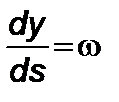 , где
, где 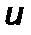 ,
, 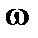 – некоторые безразмерные координаты; наконец, обозначим первый член в (2.3.6) с учетом (5.3.1) как
– некоторые безразмерные координаты; наконец, обозначим первый член в (2.3.6) с учетом (5.3.1) как

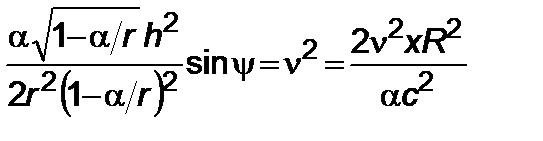 , (5.3.2)
, (5.3.2)
где 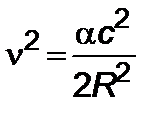 – отношение силы тяжести на начальной орбите к радиусу
– отношение силы тяжести на начальной орбите к радиусу 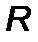 . Далее примем
. Далее примем

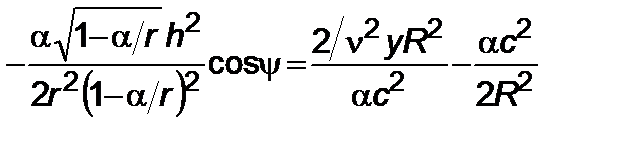 , (5.3.3)
, (5.3.3)
пренебрегая вторым членом в (2.3.2), получим окончательно

 , (5.3.4)
, (5.3.4)

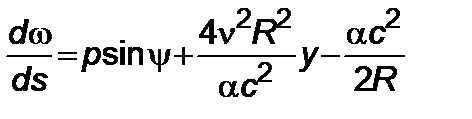 , (5.3.5)
, (5.3.5)
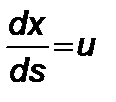 , (5.3.6)
, (5.3.6)
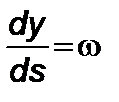 . (5.3.7)
. (5.3.7)
Далее решается вариационная задача о нахождении функции 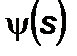 при заданных граничных условиях, дающих максимум высоты
при заданных граничных условиях, дающих максимум высоты
|
|
|
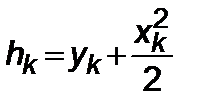 . (5.3.8)
. (5.3.8)
Задача на условный экстремум с дифференциальными связями решается просто: составляется функция Лагранжа
 , (5.3.9)
, (5.3.9)
где  – некоторые дифференцируемые функции от
– некоторые дифференцируемые функции от  . Обратим внимание, что в поле гравитации
. Обратим внимание, что в поле гравитации 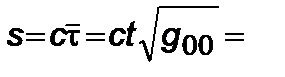
 , таким образом, время
, таким образом, время 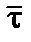 (или интервал
(или интервал  ) зависит от гравитационного радиуса
) зависит от гравитационного радиуса 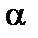 . Итак, из (5.3.4)¸(5.3.7) имеем
. Итак, из (5.3.4)¸(5.3.7) имеем

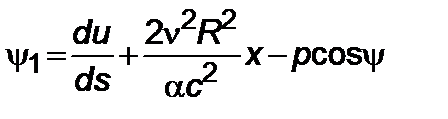 , (5.3.10)
, (5.3.10)

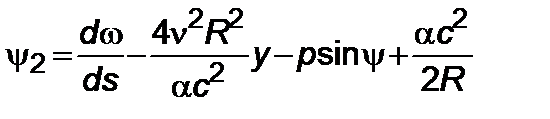 , (5.3.11)
, (5.3.11)
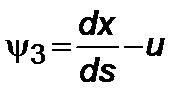 , (5.3.12)
, (5.3.12)
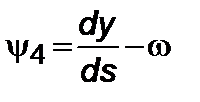 . (5.3.13)
. (5.3.13)
Функционал, максимум которого будем искать, имеет вид
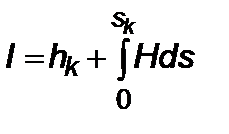 . (5.3.14)
. (5.3.14)
Запишем первую вариацию для 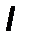
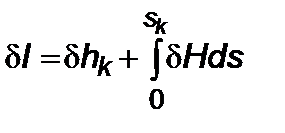 , (5.3.15)
, (5.3.15)
где
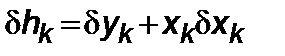 .
.
Экстремальное значение функционала 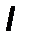 соответствует равенству нулю его первой вариации
соответствует равенству нулю его первой вариации 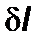 . Приравнивая нулю множители, стоящие под знаком интеграла перед вариациями
. Приравнивая нулю множители, стоящие под знаком интеграла перед вариациями 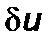 ,
, 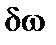 ,
, 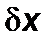 ,
, 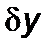 , получим систему дифференциальных уравнений для величин
, получим систему дифференциальных уравнений для величин 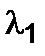 ,
, 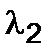 ,
,  ,
, 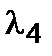 и конечные соотношения для
и конечные соотношения для 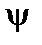
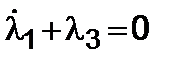 , (5.3.16)
, (5.3.16)
|
|
|
 , (5.3.17)
, (5.3.17)
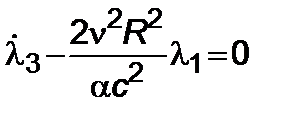 , (5.3.18)
, (5.3.18)
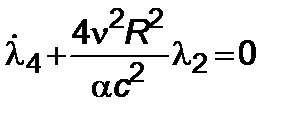 , (5.3.19)
, (5.3.19)
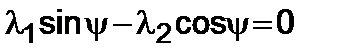 . (5.3.20)
. (5.3.20)
Из последнего уравнения
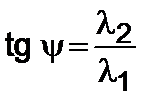 . (5.3.21)
. (5.3.21)
Решение (5.3.17–5.3.20) имеет вид (для 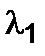 ,
, 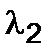 )
)
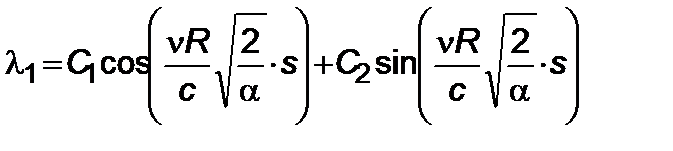 , (5.3.22)
, (5.3.22)
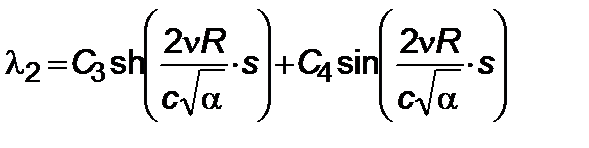 . (5.3.23)
. (5.3.23)
Таким образом, функция 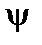 (угол тангажа) есть
(угол тангажа) есть
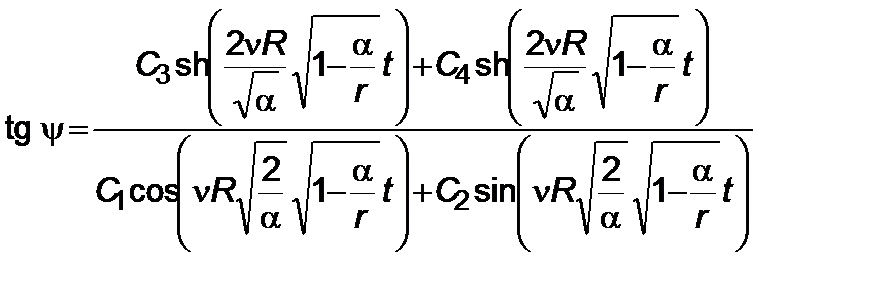 . (5.3.24)
. (5.3.24)
Из (5.3.24) видно, что угол тангажа в третьей зоне зависит не только от времени удаленного наблюдателя 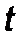 , но и от отношения гравитационного радиуса
, но и от отношения гравитационного радиуса 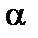 к радиусу
к радиусу  , которая также зависит от времени
, которая также зависит от времени 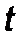 . Другими словами, зависимость
. Другими словами, зависимость 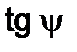 от времени, в отличие от ньютоновского подхода – нелинейная.
от времени, в отличие от ньютоновского подхода – нелинейная.
5.4. Вопросы устойчивости ракеты (зонда) вблизи “черной дыры”
При подлете к сколлапсированной звезде следует учитывать особенности допустимых орбит. Уже в 1949 году астрофизиком Л.Капланом [22] было доказано, что ближе, чем на три гравитационного радиуса, нельзя подходить к звезде, поскольку не существует устойчивых орбит. Зонд может быть, как было отмечено выше, “поглощен” “черной дырой”, сразу или после многократного вращения, может быть выкинут из орбиты по гиперболе – все зависит от момента количества движения ракеты. Оказывается, устойчивы круговые орбиты 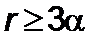 , на которых можно изучать характеристики “черной дыры”. Покажем это на примере движения ракеты при воздействии постоянного радиального реактивного ускорения
, на которых можно изучать характеристики “черной дыры”. Покажем это на примере движения ракеты при воздействии постоянного радиального реактивного ускорения 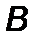 . Из уравнения (2.3.8) следует интеграл
. Из уравнения (2.3.8) следует интеграл
|
|
|
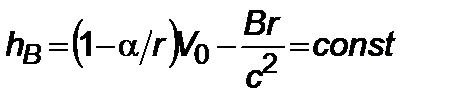 . (5.4.1)
. (5.4.1)
Комбинируя (5.4.1) с интегралом
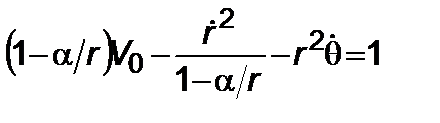 (5.4.2)
(5.4.2)
и интегралом
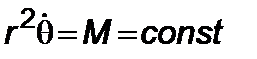 , (5.4.3)
, (5.4.3)
получим при 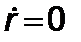 (круговая орбита) для квадрата эффективной энергии
(круговая орбита) для квадрата эффективной энергии 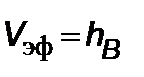
 (5.4.4)
(5.4.4)
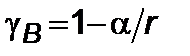 .
.
Дифференцируя (5.4.4) по 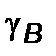 и приравнивая нулю, получим выражения для минимального значения
и приравнивая нулю, получим выражения для минимального значения 
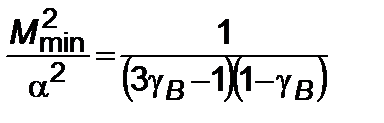 ; (5.4.5)
; (5.4.5)
видно, что 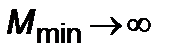 , когда
, когда 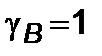 ,
, 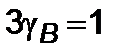 , а эффективная энергия
, а эффективная энергия
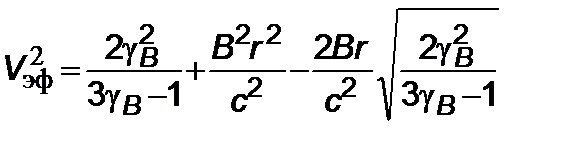 . (5.4.6)
. (5.4.6)
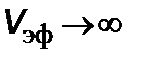 , когда
, когда  ,
, 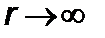 . Дифференцируя (5.4.6), имеем
. Дифференцируя (5.4.6), имеем
 ,
, 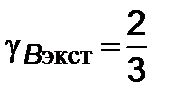 ,
, 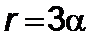 . (5.4.7)
. (5.4.7)
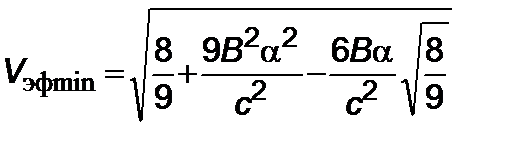 , (5.4.8)
, (5.4.8)
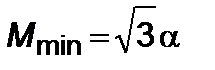 . (5.4.9)
. (5.4.9)
Таким образом, при 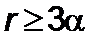 орбита устойчивая, и траектория ракеты (зонда) должна выбираться выше этого предела.
орбита устойчивая, и траектория ракеты (зонда) должна выбираться выше этого предела.
Дата добавления: 2019-01-14; просмотров: 190; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
