Городская математическая олимпиада (2004 год)
Условия задач
8 класс
1. Известен старинный способ умножения чисел, близких к 100. Находятся дополнения каждого из чисел до 100. Затем от одного из чисел вычитается дополнение другого числа и к полученному результату приписывается произведение дополнений. Например, произведение 98×93 находится так: дополнение 98 равно 2, дополнение 93 равно 7; 98-7=93-2=91; 2×7=14; получаем 98×93 = 9114. Обоснуйте правильность этого способа.
2. Доказать, что в любой трапеции разность боковых сторон меньше разности оснований.
3. Точка Р лежит внутри правильного треугольника АВС со стороной 1. Точки К, L и М – основания перпендикуляров, опущенных из точки Р на стороны ВС, АС и АВ соответственно. Найти PК+PL+PM.
4. В трех сосудах содержится по 100 г растворов кислоты: в первом 70-процентный, во втором - 60-процентный, в третьем – 50-процентный. Можно ли, смешивая эти растворы, получить 250 г 59-процентного раствора кислоты?
5. Имеются две лучи камней. Два игрока забирают поочередно камни. Разрешается взять один из любой кучки или по одному из обеих кучек. Проигравшим считается тот, кто не сможет сделать хода. Когда выгодно сделать первый ход, а когда предоставить право первого хода сопернику?
6. Математик XIX столетия де Морган на вопрос о том, когда он родился, отвечал: в х2 году мне было х лет. В каком году родился де Морган?
7. Можно ли числа 0, 1, 2, 3. 4, 5, 6, 7, 8 и 9 расставить по кругу так, чтобы разность между любыми двумя соседними числами составляла 3, 4 или 5?
|
|
|
9 класс
1. Будет ли число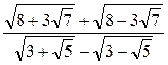 
рациональным?
2. Через центр вписанной в треугольник АВС окружности проведена прямая, параллельная стороне АС и пересекающая стороны АВ и ВС в точках M и N соответственно. Докажите, что MN = AM + NC.
3. См. задачу 5 для 8 классов.
4. См. задачу 4 для 8 классов.
5. Сократима ли дробь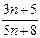 
при каком-нибудь натуральном значении n?
6. Окружности пересекаются в точках А и В. Некоторая прямая пересекает первую окружность в точках С и Е, а вторую – в точках D и F(точки D и Е расположены между С и F). Докажите, что углы САD и FВЕ равны.
7. Дано n чисел, каждое из которых равно 1 или – 1. Известно, что х1х2+х2х3+…+xnx1=0. Докажите, что n делится на 4.
10 класс
1. Решите уравнение (х2+4х)2+(х+2)2–10 = 0.
2. Найдите наименьшее значение выражения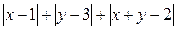 
3. Для каждого значения параметра определить число решений уравнения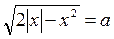 
4. Точка Р лежит внутри правильного треугольника АВС со стороной 1. Точки К, L и М – основания перпендикуляров, опущенных из точки Р на стороны ВС, АС и АВ соответственно. Найти ВК+CL+AM.
5. На сторонах ВС и CD квадрата ABCD со стороной 1 взяты точки M и N так, что угол MAN равен 45°. Найти периметр треугольника CMN.
6. Может ли 5n-1 делиться на 4n-1 при каком-нибудь натуральном n?
|
|
|
7. Дано n чисел, каждое из которых равно 1 или – 1. Известно, что х1х2+х2х3+…+xnx1=0. Докажите, что n делится на 4.
11 класс
1. В кубе ABCDA1B1C1D1, длина ребра которого рана 1, построить сечение, проходящее через середины ребер АВ, ВС и СС1 и найти его площадь.
2. Сократима ли дробь 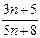при каком-нибудь значении n?
3. Решить уравнение (х2-х-1)2 = х3+5
4. Найти наибольшее значение выражения 3х+у при условии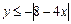 
.
5. Найти f(x), если при всех х выполнено равенство 2f(x–1)+3f(1–x) = x2.
6. Замкнутая линия на плоскости такова, что у любого вписанного в нее четырехугольника сумма противоположных углов равна 180°. Докажите, что эта линия – окружность.
7. Можно ли квадрат размером 10х10 клеток составить из фигурок, каждая из которых представляет собой 4 клетки, расположенные в форме буквы Т.
Решения.
8 класс
1. Обозначим числа через а и b. Тогда (a – (100–b))×100 + (100–a)×(100–b) = 100a–10000+100b+10000–100a–100b+ab = ab.
2. Пусть в трапеции ABCD большее основание – AD, а большая боковая сторона – АВ. Проведем отрезок ВКïçCD. Тогда АВ < BK + AE. Учитывая, что АЕ = AD – BC, а ВК = CD, получим AB – CD < AD – BC.
3. Из равенства SABC = SAPB + SBPC + SCAP следует, что АВ×h = АВ×РМ + ВС×РК + АС×PL, где h – высота треугольника АВС. Так как треугольник АВС равносторонний, то получаем, что PК+PL+PM = h =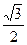 
.
|
|
|
4. Для получения 250 г раствора наибольшей концентрации надо смешать 100 г 70-процентного раствора, 100 г 60-процентного и 50 г 30-процентного. Всего в новом растворе будет содержаться 100×0,7 + 100×0,6 + 50×0,3 = 145 г кислоты, то есть его концентрация будет 58%. Значит 59-процентный раствор получить невозможно.
5. Игрок своим ходом может менять четность числа камней в одной кучке или в двух кучках сразу. Поэтому позиции, при которых в каждой кучке четное число камней, проигрышны для того игрока, чья очередь делать ход. Поэтому первый ход выгодно сделать, когда хотя бы в одной из кучек лежит нечетное число камней.
6. 422 = 1764, 432 = 1849, 442 = 1936. Так как де Морган жил в ХIX столетии, то ему было 43 года в 1849 году. То есть родился он в 1806 году.
7. Нельзя. Допустим, что указанная расстановка возможна. Тогда никакие из чисел 0, 1, 2, 8 и 9 не должны стоять рядом. Так как всего имеется 10 чисел, то перечисленные пять чисел должны чередоваться с числами 3, 4, 5, 6 и 7. То есть два числа из первой пятерки будут соседями числа 7. Но по условию задачи число 7 не должно стоять рядом с числами 0, 1, 8 и 9. Получили противоречие.
9 класс
1. Возведем данное число в квадрат и получим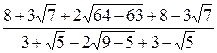 
= 
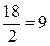. Так как данное число, очевидно, положительное, то оно равно 3.
|
|
|
2. Пусть точка О – центр вписанной окружности. Тогда АО и СО – биссектрисы, откуда, учитывая, что MNïêАС, получим, что треугольники АМО и CNO равнобедренные. Таким образом MN = MO + ON = AM + MC.
3. См. решение задачи 5 для 8 класса
4. См. решение задачи 4 для 8 класса
5. Пусть 3n+5=pm, 5n+8=qm, где p, q, m – натуральные числа. Вычтем из первого равенства второе, предварительно умножив обе части первого равенства на 5, а второго – на 3. Получим, что 1 = m(5p–3q). Последнее равенство возможно лишь при m = 5p–3q =1. То есть числитель и знаменатель данной дроби не могут иметь общего множителя, отличного от 1. Тем самым дробь несократима.
6. ÐFBE = ÐFBA – ÐABE = ÐFDA – ÐACE = ÐCAD
7. Расставим числа по кругу. Тогда сумма произведений соседних чисел равна 0. Разобьем числа на группы стоящих рядом одинаковых чисел. Пусть имеется m таких групп. При перемножении чисел из соседних групп получается –1, при перемножении чисел из одной группы получается 1. Нетрудно понять, что –1 получится столько раз, сколько имеется групп, то есть m раз. Но так как общая сумма равна 0, а всего слагаемых n, то m = 0,5n или n = 2m. Кроме того, группы, состоящие из 1 и –1, чередуются, поэтому число m должно быть четным. Откуда следует, что n делится на 4.
10 класс
1. Раскроем вторые скобки и сделаем замену t = x2+4x, после чего получим уравнение t2+t–6 = 0, корни которого t1=2 и t2= –3. Решая теперь уравнения x2+4x = 2 и x2+4x = –3, получим 4 корня исходного уравнения: –1, –3,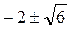 
.
2. 
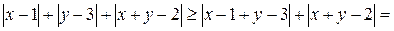
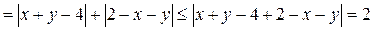. С другой стороны, при х=1, у=3 значение данного выражения равно 2. Поэтому 2 – его наименьшее значение.
3. Рассмотрим функцию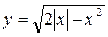 
. Данное равенство равносильно системе 
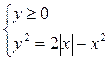. При х³0 получаем у2+(х–1)2=1, что с учетом условия у³0 дает нам верхнюю половину окружности радиуса 1 с центром в точке (1;0). При х£0 получаем симметричную относительно оси OY полуокружность. Потому график функции 
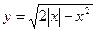выглядит так:
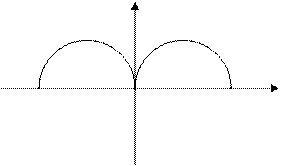
Из графика видно, что при a>1 и при a<0 исходное уравнение не имеет корней, при а=1 – 2 корня, при а=0 – 3 корня, при 0<a<1 – 4 корня.
4. Проведем через точку Р отрезки, параллельные сторонам треугольника АВС. Они разобьют треугольник АВС на три параллелограмма и три равносторонних треугольника. Нетрудно заметить, что сумма отрезков ВК, CL и АМ в два раза меньше суммы периметров этих треугольников, а сумма периметров треугольников, в свою очередь, равна периметру треугольника АВС. То есть ВК+CL+АМ = 1,5.
5. 
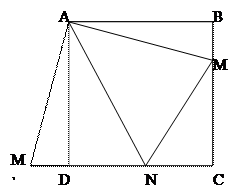«Отрежем» от квадрата треугольник АВМ и «приставим» его с другой стороны, так чтобы сторона АВ совместилась со стороной AD. Заметим, что ÐМ1AN = ÐМ1AD + ÐDAN = ÐBAM + ÐDAN = 90°–ÐMAN = 45° = Ð MAN. Отсюда получаем равенство треугольников M1AN и MAN, откуда MN = MN1. Поэтому PMNC = MC+CN +MN = MC+CN +M1N = MC+CN+DN+M1D = MC+CN+DN+BM = BC +CD = 2.
6. Если n четное, т.е. n=2m, то 42m-1 = 16m-1 делится на 5, а 5n-1 не делится на 5. Если n нечетное, т.е. n=2m+1, то 4n=4×16m-1=3×16m+(16m-1) делится на 3, а 5n=5×25m-1=5×(25m-1)+3+1 имеет при делении на 3 остаток 1. То есть 5n-1 не может делиться на 4n-1 ни при каких n.
7. Смотрите решение задачи 7 для 9 класса.
11 класс
1. Нетрудно доказать, что данное сечение будет правильным шестиугольником со стороной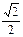 
. Тогда его площадь равна 
.
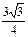2. Смотрите решение задачи 7 для 9 класса.
3. (х2–х–1)2 = х3+5 Û (х2–х–1)2 –4= х3+1 Û(х2–х–3)(х2–х+1)=(х+1)(х2–х+1). Так как х2–х+1>0 при всех значениях х, то х2–х–3=х+1, то есть х2–2х–4=0. Таим образом,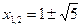 
.
4. Пусть 3х+у = а, тогда у = а–3х, и исходное неравенство примет вид: а £ 3х–ï8–4хô. Построим график функции а = 3х–ï8–4хô. Если х³2, то а = 8–х; если х£2, то а = 7х–8. Из графика видно, что наибольшее значение, которое может принимать а (а, значит, и 3х+у) равно 6.
5. Нельзя. Раскрасим клетки квадрата в черный и белый цвет как шахматную доску. Если квадрат можно составить из указанных в условии фигурок, то, во-первых, таких фигурок надо взять 25 штук, во-вторых, каждая из них должна покрывать нечетное количество черных клеток (1 или 3). Сумма 25 нечетных чисел нечетна, а всего черных клеток 50. Противоречие.
6. Так как равенство 2f(x–1)+3f(1–x) = x2 выполняется при всех х, то в нем можно х заменить на 2–х, после чего мы получим: 2f(1–x)+3f(x–1)= (2–x)2. Вместе с исходным уравнением полученное уравнение составляет линейную систему относительно f(x–1) и f(1-x). Решая эту систему, получим: f(x-1) = 0,2x2-2,4x+2,4. Отсюда окончательно получим f(x) = f(x+1-1)= 0,2(x+1)2-2,4(x+1)+2,4 = 0,2x2-2x+0,2.
7. Рассмотрим какой-нибудь вписанный в линию четырехугольник ABCD, зафиксируем вершины А, В и С, а вершину D начнем двигать по «дуге» СDА. При этом угол В не будет меняться, а, значит, не будет изменяться и угол D, что следует из условия задачи. А это означает, что «дуга» СDА – дуга окружности (геометрическое место точек, из которых данный отрезок виден под данным углом). Теперь начнем двигать по дуге АBС точку В и придем к выводу, что это тоже дуга окружности, опирающаяся на ту же хорду АС. При этом градусные меры дуг СDА и АBС дают в сумме 360°, откуда следует, что это дуги одной и той же окружности.
Дата добавления: 2019-01-14; просмотров: 125; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!