Анализ решения оптимизационной задачи

Никогда не стоит принимать окончательное решение оптимизационной задачи без результатов ее анализа. В качестве главного средства анализа используется математическая модель, позволяющая выполнить параметрический, структурный и многокритериальный анализ задачи.

Параметрическим называется такой анализ, при котором задача решается многократно при различных значениях некоторого исходного данного (параметра). Оценивается влияние этого параметра на результаты решения.

При структурном анализе многократное решение задачи выполняется при различной структуре ограничений и граничных условий. Оценивается влияние ограничений и граничных условий на результаты решения.

Решение задачи по различным критериям (с различными целевыми функциями) составляет суть многокритериального анализа.

Окончательное решение задачи принимается после исследования всех решений, полученных при параметрическом, структурном и многокритериальном анализах.

В качестве примера составления математической модели рассмотрим задачу распределения ресурсов. Под ресурсами понимают, например финансы, энергию, сырье, необходимые для выпуска продукции и получения в конечном итоге прибыли. Естественно стремятся к максимальной прибыли при ограниченном количестве ресурсов.

Пример 1. Определить максимальную прибыльпредприятия,

выпускающего продукцию в виде изделий трех видов (i = 1, 2, 3). Для изготовления каждогоi-гоизделия требуются три вида ресурсов: энергетические, финансовые и сырьевые (j = 1, 2, 3).

Исходные данные:

11

наличие на предприятии каждого j-горесурсаb j; норма расходаj-горесурса на одно изделиеi-говидаa ji; прибыльz i от реализации одногоi-гоизделия;

минимальное количество b4 всех видов изделий, которое предприятие должно выпустить.

Решение. Обозначим искомые количества1-го,2-гои3-говидов

изделий через х1, х 2 их3.

Поскольку необходимо найти максимальную прибыль предприятия, этот экономический критерий и выразим целевой функцией. Прибыль от реализации изделий i-говида есть произведениеzi xi. Подлежащая максимизации суммарная прибыль от реализации трех видов изделий (целевая функция) будет иметь

следующий вид:
Z = z 1 x 1 + z 2 x 2 + z 3 x 3 → max.	(1.4)

Перейдем к составлению ограничений. Поскольку на одно изделие 1-говида требуетсяа11 единиц энергии, на искомое количествох1 потребуетсяа11х1 единиц энергии. Для искомых количеств изделий2-гои3-говидов потребуется соответственноа12х2иа13х3 единиц энергии. Суммарный расход энергии на выпуск трех видов изделий составита11х1 +а12х2 +а13х3 единиц энергии. Эта величина ограничена наличием на предприятии энергетических ресурсов в количествеb1. Таким образом, ограничение по энергетическим ресурсам будет иметь вид

а11х1+ а12х2+ а13х3< b1.

Аналогично составляются ограничения по финансовым и сырьевым ресурсам.

Ограничение минимального суммарного количества выпускаемых изделий запишется как

х 1 + х 2 + х 3 > b 4 .

В итоге, вся система ограничений будет иметь вид

а 11 х 1 + а 12 х 2 + а 13 х 3 < b 1 ,
а 21 х 1 + а 22 х 2 + а 23 х 3 < b 2 ,	(1.5)
а 31 х 1 + а 32 х 2 + а 33 х 3 < b 3 ,
х 1 + х 2 + х 3 > b 4 .

 

11. Решение ЛП-задачи графическим методом.

 

I. Вограничениях задачи замените знаки неравенств на знаки точных равенств и постройте соответствующие прямые.

II. Найдите и заштрихуйте полуплоскости, разрешенные каждым из ограничений-неравенств задачи. Для этого подставьте в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверьте истинность полученного неравенства.

Если неравенство истинное, то надо заштриховать полуплоскость, содержащую данную точку; иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.

Поскольку х1и х2 должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси х₁ и правее оси х2, т.е. в 1-м квадранте.

Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой, поэтому выделите на графике такие прямые.

1. Определите ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделите ее. При отсутствии ОДР задача не имеет решений, о чем сделайте соответствующий вывод.
2. Если ОДР - не пустое множество, то постройте целевую прямую, т.е. любую из линий уровня с₁х₁ + с₂х₂ = L, где L - произвольное число, например, кратное с₁и с₂, т.е. удобное для проведения расчетов. Способ построения аналогичен построению прямых ограничений.

V. Постройте вектор C = (c₁,с₂), который начинается в точке (0;0), заканчивается в точке (c₁,с₂). Если целевая прямая и вектор С построены верно, то они будут перпендикулярны.

VI. При поиске max ЦФ передвигайте целевую прямую в направлении вектора С, при поиске min ЦФ - против направления вектора С. Последняя по ходу движения вершина ОДР будет точкой max или min ЦФ. Если такой точки (точек) не существует, то сделайте вывод о неограниченности ЦФ на множестве планов сверху (при поиске шах) или снизу (при поиске min).

Определите координаты точки max (min) ЦФ X = (х1^*; х2^*) и вычислите значение ЦФ l(x^*). Для вычисления координат оптимальной точки X^* решите систему уравнений прямых, на пересечении которых находится X^* .

Задача 1

Найдем оптимальное решение задачи, математическая модель которой имеет вид

L(Х) = 3x₁ + 2x₂ → max

х₁+ 2х₂ < 6, (1)

2х₁+ х₂ < 8, (2)

-х₁+х₂<1, (3)

х₂ < 2, (4)

х₁>0,х₂>0.

Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат (рис. 2 ).

х₁+ 2х₂ = 6,(1)

2х1 +х2= 8,(2)

-х1+х2= 1,(3)

х2= 2. (4)

(1) х1=0, х1=6, х2=3, х2=0,

(2) х1=0, х1=4, х2=8, х2=0,

(3) х1=0, х1=-1, х2=1, х2=0,

Прямая (4) проходит через точку х₂ = 2 параллельно оси L(Х).

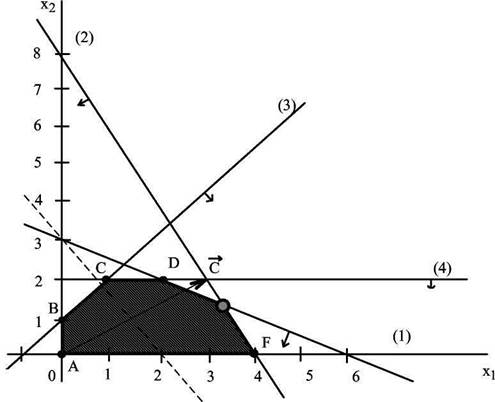
Рис. 2. Графическое решение задачи

Определим ОДР. Например, подставим точку (0;0) в исходное ограничение (3), получим 0 < 1, что является истинным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (3). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (рис. 2). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник ABCDEF.

Целевую прямую можно построить по уравнению

3х1 +2x2 ⁼6,

Х1=0, х1=2,

Х2=3, х2=0,

Строим вектор С из точки (0;0) в точку (3;2). Точка Е- это последняя вершина многоугольника допустимых решений ABCDEF, через которую проходит целевая прямая, двигаясь по направлению вектора С. Поэтому Е -это точка максимума ЦФ. Определим координаты точки Е из системы уравнений прямых ограничений (1) и (2)

_Х1+2х₂=6, (1) х1=10/3=3 1/3, х2=4/3=1 1/3

2_Х1+х₂=8, (2) Е 3 1/3; 1 1/3

Максимальное значение ЦФ равно L(E) = 3*10/3+2*4/3 = 12 2 / 3

 

 

12. Понятие симплекс-метода.

 

Оптимальное решение задачи линейного программирования (ЗЛП) связаны с угловыми точками многогранника решений.

Угловых точек может быть много, если много ограничений. Количество угловых точек соответствует количеству базисных решений. Для каждого базисного решения однозначно определяется значение целевой функции.

Найти оптимальное решение (оптимальный план), беспорядочно перебирая все базисные решения, затруднительно.

В связи с этим необходим такой переход от одного базисного решения к другому (от одной угловой точки к другим точкам, начиная с угловой точки, отвечающей исходному базисному решению), в результате которого новое решение приносило бы большее значение целевой функции, причем максимально возможное увеличение.

Данный процесс решения задачи реализуется симплекс-методом (методом последовательного улучшения плана). Процесс решения задачи продолжается до получения оптимального плана, либо до установления факта, что решения нет. Переход от одного базисного решения к другому называется итерацией симплекс-метода.

Для того чтобы ЗЛП была решаема (имела оптимальное решение), необходимо и достаточно, чтобы ограничения задачи были совместимыми, чтобы множество допустимых значений существовало, и целевая функция должна быть ограничена при поиске максимума - сверху и минимума - снизу.

Симплекс - метод может быть интерпретирован геометрически как движение по соседним угловым точкам многогранника решений (если они расположены на одном ребре - то соседние). Следовательно, количество итераций симплекс-метода зависит от выбора исходного базисного плана и количества угловых точек, встречающихся при движении от исходного к оптимальному плану.

Пример 2.3:

f(x) = 12x₁ + 15x₂®max

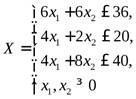
Приводим к канонической форме:

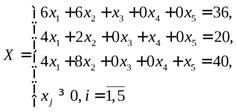
f(x) = 12x₁+15x₂ +0x₃+0x₄+0x₅

Среди переменных задачи можно выделить базисные переменные x₃, x₄, x₅ и не базисныеx₁,x₂.

Не базисные те, которые можно приравнять к 0, а остальные базисные.

Приравняв не базисные переменные к 0, получим исходный базисный план:

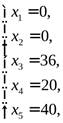
Значение целевой функции для этого плана f(x) = 0 (прибыль равна нулю)

Данная ситуация не может удовлетворить предприятие, и, тем более, не является оптимальной.

f(x)= 0-(-12x₁-15x₂)®max

Анализируя функцию fможно сделать вывод, что увеличение значения функции (дохода) может произойти только при возрастании значений х₁ иx₂, отсюда увеличение х₁ илиx₂равносильно переходу переменных в число базисных.

В первую очередь увеличиваем значение x₂, так как единица продукции Р₂приносит больший доход. Значение х_1, по-прежнему, равно 0 , значениеx₂ нельзя увеличивать бесконечно, то есть увеличиваем до тех пор, пока х₃,x₄иx₅ ≥ 0. Значит, необходимо определить значениеx₂, до которого можно его увеличивать:

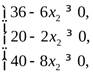
Для выполнения данных условий необходимо чтобы x₂=5, так как данное значение получилось из 3-го ограничения, то, выразивx₂ черезx₁иx₅, мы заменим (введем) переменнуюx₂в число базисных вместоx_5.

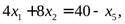
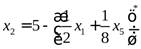
Подставим выражение x₂в целевую функцию и оставшиеся ограничения поx₃иx₄:

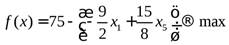
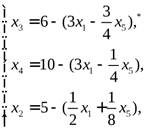
В этом случае новый базисный план после первой итерации будет:

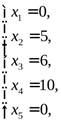
f(x) = 75

На основании результатов можно сделать вывод, что полученный план не является оптимальным, так как значение целевой функции может быть увеличено за счет увеличения значения x₁ (x₅мы не можем увеличивать, так как это приведет к снижениюf).

Значение x₁также нельзя увеличивать бесконечно, а только до такой величины, чтобыx₃,x₄,x₂ ≥ 0:

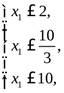
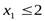- из первого ограничения.

x₁выразим из 1-го ограничения:

,

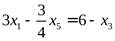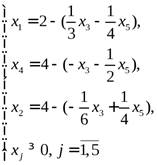
В этом случае новый базисный план после второй итерации будет:

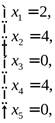
f(x)=84

После анализа значения fследует, что данный план является оптимальным так как х₃ и х₅ 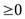, то на основании оптимального плана (f*= 84,x₁* = 2x₂*= 4) делаем вывод, что предприятие для получения максимального дохода, равного 84 единицы должно выпускать из имеющегося количеств сырья 2 ед. продукции Р₁и 4 ед. продукции Р₂.

Пример 2.4:

Найдем наибольшее значение функции в заданной области, т.е. решим задачу линейного программирования (максимизируем линейную функцию при линейных ограничениях).

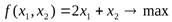
Приводим к канонической форме:

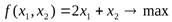
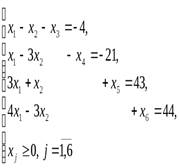
			х2
						(1) (4)
				(3)
					(2)
							х1

рис . 2.2

.

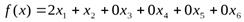1)Среди переменных задачи можно выделить базисные переменныеx₃, x₄,x₅,x₆ и не базисныеx₁, x₂.

Приравняв не базисные переменные к 0, получим исходный базисный план:

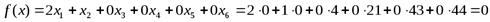
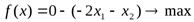
В первую очередь увеличиваем значение x₁, т.к. единица продукцииP₁ приносит больший доход. Значение х₂, по-прежнему, равно 0, однако значениеx₁ нельзя увеличивать бесконечно, т.е. увеличиваем до тех пор, пока х₃, x₄,x₅ и x₆ ≥ 0. Значит, необходимо определить значениеx₁, до которого можно его увеличивать.

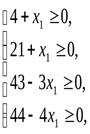
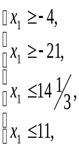
Для выполнения данных условий необходимо чтобы x₁=11, т.к. данное значение получилось из четвертого ограничения, то, выразивx₁ черезx₂иx₆, мы введем переменнуюx₁в число базисных вместоx₆.

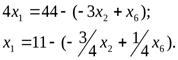
Подставим выражение x₁в целевую функцию и оставшиеся ограничения поx₃,x₄ иx₅.

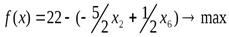
2)В этом случае новый базисный план после первой итерации будет:

.

На основании результатов можно сделать вывод, что полученный план не является оптимальным, т.к. значение целевой функции может быть увеличено за счет увеличения значения x₂ (x₆мы не можем увеличивать т.к. это приведет к снижению значения целевой функции).

Значение x₂ нельзя увеличивать бесконечно, т.е. увеличиваем до тех пор, пока х₃, x₄,x₅ и x₁ ≥ 0.

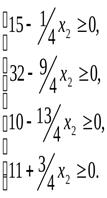
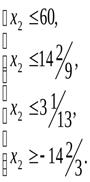
Выразив x₂ черезx₅иx₆, мы введем переменнуюx₂в число базисных вместоx₅.

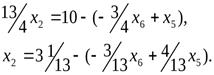
Подставим выражение x₂в целевую функцию и оставшиеся ограничения поx₃,x₄ иx₁.

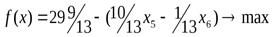
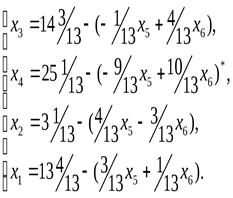
3)В этом случае новый базисный план после второй итерации будет:

.

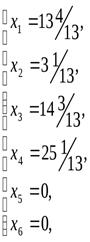
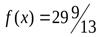Полученный план не является оптимальным, т.к. значение целевой функции может быть увеличено за счет увеличения значения x₆ (x₅мы не можем увеличивать т.к. это приведет к снижению значения целевой функции).

Значение x₆ увеличиваем до тех пор, пока х₃, x₄,x₂ и x₁ ≥ 0.

Выразив x₆ черезx₄иx₅, мы введем переменнуюx₆в число базисных вместоx₄.

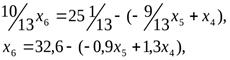
Подставим выражение x₆в целевую функцию и оставшиеся ограничения поx₃,x₂ иx₁.

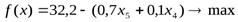
4)В этом случае новый базисный план после третьей итерации будет:

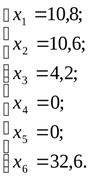
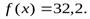
После анализа значения fследует, что данный план является оптимальным т.к. все .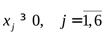

Ответ: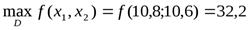

 

13. Решение ЛП-задачи с помощью электронных таблиц Excel.

 

Для решения задач линейного программирования в программе Excel имеется надстройка Поиск решения,обращение к которой производится из меню Сервис.

Если команда Поиск решения отсутствует в меню Сервис, то требуется установить надстройку «Поиск решения». Для этого в менюСервис выбирается команда Надстройки, которая открывает диалоговое окно, показанное на рис. 1.

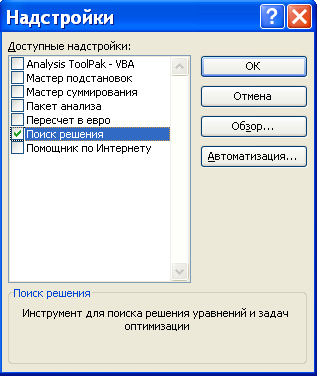
Рис. 1

Далее в этом окне устанавливается флажок той надстройки, которую необходимо загрузить, и нажимается кнопка OK.

Покажем использование надстройки «Поиск решения» на примере решения следующей задачи.

Постановка задачи

Предприятие изготавливает и реализует три вида продукции – P₁, Р₂ и Р₃. Для производства продукции используются три вида ресурсов – комплектующие изделия, сырье и материалы. Запасы ресурсов и их расход на изготовление единицы продукции каждого вида приведены в таблице 1.

Прибыль от реализации единицы продукции каждого вида составляет 240, 210 и 180 денежных единиц для P₁, Р₂ и Р₃ соответственно.

Требуется определить производственную программу предприятия таким образом, чтобы прибыль от реализации продукции был максимальным.

Таблица 1

Виды ресурсов	Расходы ресурсов на 1 ед. продукции			Запасы Ресурсов, ед.
	P1	P2	P3
Комплектующие изделия	4	6	8	3120
Сырье	2	8	10	3000
Материалы	6	9	4	3150

Математическая модель задачи

Обозначим переменными x₁, x₂ и x₃ искомые объемы производства продукции видов P₁, Р₂ и Р₂, а через F – прибыль предприятия. Тогда математическая постановка представленной задачи принимает следующий вид.

Определить значения переменных x₁, x₂ и x₃, для которых достигается максимум целевой функции

F = 240 x₁ + 210 х₂ + 180 x₃

при ограничениях:

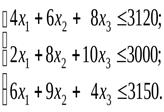
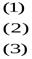
Целевая функция описывает суммарную прибыль от реализации произведенной продукции всех трех видов. Ограничения (1), (2) и (3) учитывают расход и запасы комплектующих изделий, сырья и материалов соответственно. Поскольку объемы производства продукции не могут быть отрицательными, добавляются условия

x₁ ≥ 0; x₂ ≥ 0; x₃ ≥ 0.

Порядок решения задачи

Примерные действия, необходимые для решения задачи линейного программирования средствами программы Excel, представим в виде следующей последовательности шагов.

Шаг 1. Исходные данные задачи записываются на рабочем листе электронной таблицы. Один из вариантов использования ячеек показан на рис. 2.

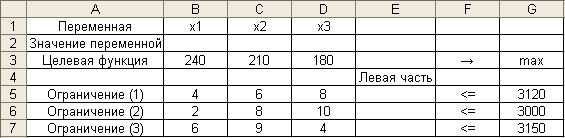
Рис. 2

Замечание. Если известно исходное допустимое базисное решение, то можно несколько ускорить процесс поиска оптимального решения. Для этого начальные значения некоторых или всех переменных могут быть заданы вручную. В данном примере для их хранения используются ячейки $B$2, $C$2 и $D$2. Если допустимое базисное решение не задано, то программа Excel автоматически определяет начальные значения переменных задачи.

Шаг 2. В ячейку E3 вводится формула

=СУММПРОИЗВ(В3:D3; $B$2:$D$2)

для вычисления текущего значения целевой функции, которая находит сумму попарных произведений ячеек (В3:D3) с коэффициентами при переменных в выражении целевой функции на ячейки ($B$2:$D$2) с текущими значениями переменных.

Шаг 3. Чтобы задать ограничения решаемой задачи, в ячейки E5, E6 и E7 копируется формула из ячейки E3. После этого в указанных ячейках должны быть получены формулы, представленные в таблице 2.

Таблица 2

Ячейка	Содержание (формула)
E5	=СУММПРОИЗВ(В5:D5; $B$2:$D$2)
E6	=СУММПРОИЗВ(В6:D6; $B$2:$D$2)
E7	=СУММПРОИЗВ(В7:D7; $B$2:$D$2)

Шаг 4. После создания таблицы с исходными данными курсор устанавливается в ячейку E3, содержащую формулу для вычисления целевой функции. Далее в меню Сервисвыбирается команда Поиск решения, которая открывает диалоговое окно, приведенное на рис. 3.

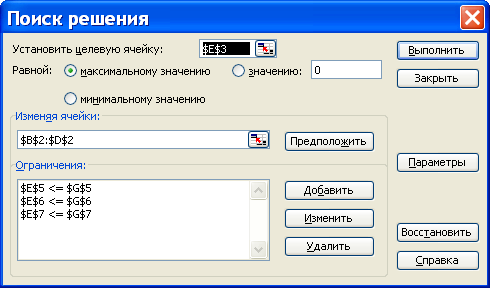
Рис. 3

В поле Установить целевую ячейку окна «Поиск решения», показанного на рис. 3, должен появиться адрес ячейки с формулой целевой функции (в данном примере это ячейка $E$3).

Затем в этом окне (рис. 3) заполняются следующие поля этого окна:

- в поле Равной переключатель вида экстремума целевой функции устанавливается в положение максимальное значение (или минимальное значениепри соответствующей постановке задачи);

- в поле Изменяя ячейкиуказывается диапазон ячеек со значениями переменных задачи, выделив его на рабочем листе электронной таблицы (в примере это ячейки $B$2:$D$2);

- в поле Ограничениязадаются ограничения исходной задачи. Для этого курсор устанавливается в поле ввода ограничений и нажимается кнопку Добавить. В результате выводится диалоговое окно «Добавление ограничения», показанное на рис. 4.

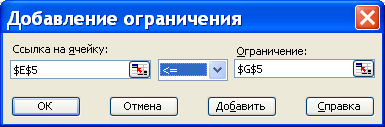
Рис. 4

В этом окне в поле Ссылка на ячейкувводится адрес ячейки с формулой соответствующего ограничения (например, для ограничения (1) это будет ячейка E5), а в поле Ограничение указывается предельное значение, которое может принимать выбранное ограничение (в данном примере правая часть ограничения (1) находится в ячейке G5).

Следует заметить, что заполнение полей Ссылка на ячейку и Ограничение в окне «Добавление ограничения», можно выполнить выделением соответствующих ячеек рабочего листа электронной таблицы.

Затем выбирается вид отношения, связывающего левую и правую части ограничения, что показано на рис. 5.

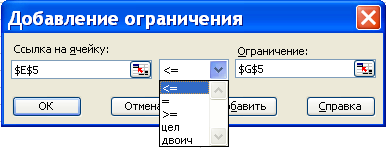
Рис. 5

После нажатия кнопки Добавить в окне «Добавление ограничения»(или кнопки ОК дляввода последнего ограничения) данное ограничение попадает в список ограничений решаемой задачи. С помощью кнопок Удалитьи Изменитьможно удалять выделенные в списке ограничения или вносить в них исправления.

Шаг 5. После заполнения всех полей окна «Поиск решения» нажимается кнопка Параметры(рис. 3), которая открывает диалоговое окно «Параметры поиска решения», показанное на рис. 6.

Рис. 6

В этом окне требуется установить флажки Линейная модельдля решения задачи линейного программирования иНеотрицательные значения,если такое условие накладываются на все переменные задачи.

Здесь (рис. 6) также можно определить параметры процесса решения: предельное время поиска решения, максимальное количество итераций, точность и т.п. Флажок Показывать результаты итераций позволяет по шагам следить за поиском решения. Флажок Автоматическое масштабированиевключается в том случае, когда разброс значений переменных очень велик.

Шаг 6. Задав необходимые параметры в окне «Параметры поиска решения», нажимается кнопка Выполнитьдля поиска решения задачи (рис. 3) в окне «Поиск решения». Если решение найдено, то на экран выводится окно с соответствующим сообщением (рис. 7).

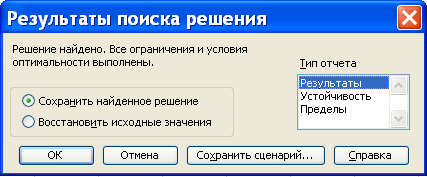
Рис. 7

Полученные результаты отображаются на рабочем листе электронной таблицы, как это показано на рис. 8. В частности, значения переменных - в ячейках $B$2:$D$2, значение целевой функции – в ячейке E3.

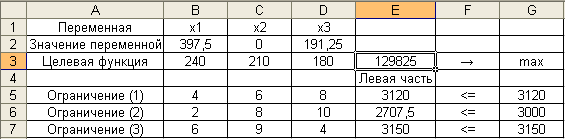
Рис. 8

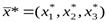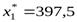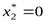Таким образом, получено оптимальное решение исходной задачи в виде вектора , где , и 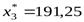, для которого значение целевой функцииF максимально и определяется как F* = 129825.

Результаты решения задачи линейного программирования также можно сохранить в виде отдельных рабочих листов с именами Отчет по результатам,Отчет по устойчивостии Отчет по пределам.Для сохранения результатов в виде отчетов необходимо предварительно в поле Тип отчетавыделить требуемые типы отчетов (рис. 7). В этом же окна можно отказаться от полученных решений и восстановить исходные значения переменных.

Отчет по результатам для рассмотренной задачи показан на рис. 9.

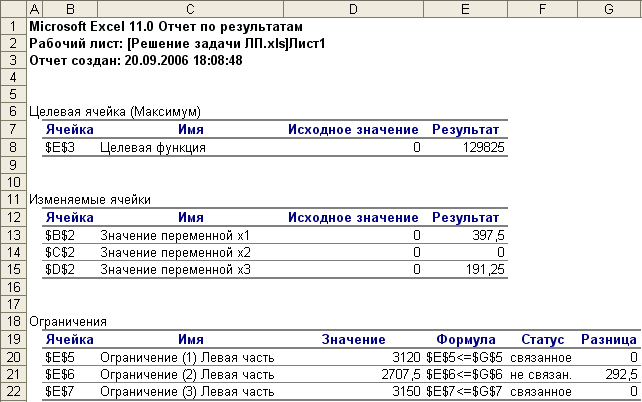
Рис. 9

В данном отчете представлено оптимальное решение задачи линейного программирования и его расположение в области допустимых решений. В графах Результатвыводятся оптимальные значения целевой функции F* и переменных задачи 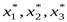, а также их значения для исходного базисного решения, с которого начинался поиск оптимального решения (графаИсходное значение).Состояние ограничений (графа Статус) характеризует расположение точки 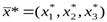в области допустимых решений. ГрафаРазница показывает разности между значениями левых и правых частей ограничений (невязки). Для связанного ограничения невязка равна нулю, что свидетельствует о расположение точки 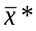на границе области допустимых решений, которая задается этим ограничением. Если ограничение являются не связанным, то оно не влияет на оптимальное решение.

Замечание. В экономической интерпретации связанные ограничения соответствуют дефицитным ресурсам. Для не связанных ограничений графа Разница показывает оставшиеся объемы неиспользованных не дефицитных ресурсов. В рассмотренной задаче ограничения (1) и (3) соответствуют комплектующим изделиям и материалам, которые являются дефицитными ресурсами. Ограничение (2) является не связанным, т.е. не влияет на оптимальный план производства продукции по критерию максимальной прибыли. Это означает, что второй ресурс (сырье) не использован в объеме 292,5 ед.

В отчет по устойчивости (рис. 10) приведены границы устойчивости переменных задачи (графы Допустимое увеличение и Допустимое уменьшение коэффициентов целевой функции), а также границы устойчивости теневых цен (т.е. переменных двойственной задачи), в пределах которых оптимальное решение не изменяется. Большие значения пределов (1Е+30) означают фактическое отсутствие соответствующих границ, т.е. переменная может изменяться до бесконечности.

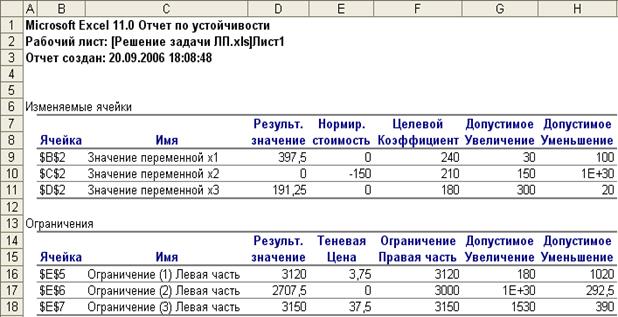
Рис. 10

В графе Нормированная стоимость элемент во второй строке (-150) показывает, на сколько уменьшится значение функции, если в решении переменную x₂ увеличить на единицу. С другой стороны, при допустимом увеличении коэффициента функции при неизвестной x₂ на 150 единиц значение этой переменной не изменится, т.е. неизвестная x₂ будет равна нулю, а если выйти за пределы допустимого увеличения (коэффициент при x₂ увеличить более чем на 150), то неизвестная x₂ в решении будет больше нуля.

В отчете по пределам (рис. 11) показаны нижние и верхние пределы возможного изменения переменных (в пределах области допустимых решений) и соответствующие значения целевой функции (графа Целевой результат) при этих изменениях. В частности, если x₁ = 0, а x₂ и x₃ остаются без изменений, то F = 240×0 + 210×0 + 180×191,25 = 34425; при x₃ = 0 и неизменных x₁ и x₂ получим F= 240×397,5 + 210×0 + 180×0 = 95400.

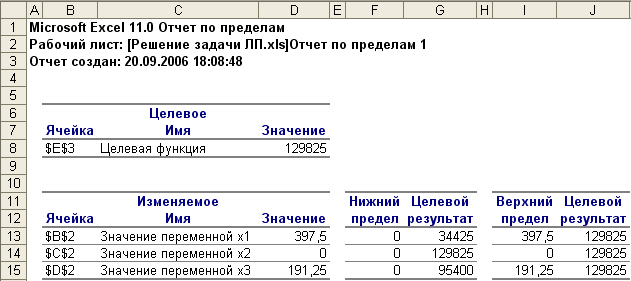
Рис. 11

Порядок выполнения работы

1. Получить у преподавателя две задачи линейного программирования. Первая задача выбирается из табл. 1, вторая – из табл. 2.

2. Решить эти задачи графическим методом (одна задача из табл. 1, вторая из табл. 2).

3. Выполнить решение каждой задачи средствами программы Excel и сравнить полученные результаты.

Замечание. Для каждой задачи в отчете должны быть представлены фрагменты рабочих листов электронной таблицы с исходными данными (пример показан на рис. 2) и полученными результатами (пример на рис. 8).

4. Для первой задачи определить исходное допустимое базисное решение и решить эту задачу симплекс-методом. Использовать табличную форму симплекс-метода.

5. Для второй задачи сначала получить исходного допустимое базисное решение методом минимизации невязок или методом искусственного базиса и завершить решение симплекс-методом.

6. Разработать программу решения задач линейного программирования симплекс-методом для случая, когда исходное допустимое базисное решение известно. Проверить работоспособность программы на примере решения первой задачи.

 

 

14. Транспортная задача, типы транспортных задач.

 

Транспортная задача линейного программирования получила в настоящее время широкое распространение в теоретических разработках и практическом применении на транспорте ив промышленности. Особенно большое значение она имеет в деле рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта.

Транспортная задача – это задача, в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.

Стандартная ТЗ определяется как задача разработки наиболее экономичного плана перевозки продукцииодного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

Пример 1. Три поставщика одного и того же продукта располагают в планируемый период следующими запасами этого продукта: первый- 120 условных единиц, второй- 100 и третий 80 единиц. Этот продукт должен быть перевезен к трем потребителям, спросы которых соответственно равны 90, 90 и 120 условных единиц. Приведенная ниже таблица содержит показатели затрат, связанных с перевозкой продукта из i-го пункта отправления в j-й пункт потребления.

Требуется перевезти продукт с минимальными затратами.

Поставщики

Потребители и их спрос Дата добавления: 2019-01-14; просмотров: 1123; Мы поможем в написании вашей работы! Поделиться с друзьями: ⇐ Предыдущая123Следующая ⇒ Мы поможем в написании ваших работ! . . © 2014-2024 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.121)