Приближенные методы решения систем линейных уравнений. Метод итерации и метод Зейделя. Условия сходимости
Итерационного процесса
Метод итерации. Постановка задачи. Пусть дана система n линейных уравнений с n неизвестными:
 (14)
(14)
или в матричном виде
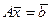 , (15)
, (15)
где A - матрица из коэффициентов системы (14)
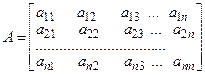 ,
,
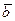 - вектор-столбец свободных членов;
- вектор-столбец свободных членов; 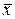 - вектор-столбец из неизвестных (искомый вектор)
- вектор-столбец из неизвестных (искомый вектор)
 ;
; 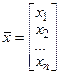 .
.
Необходимо найти такой вектор 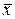 , который обращает систему (14) в тождество.
, который обращает систему (14) в тождество.
Решени е. Предполагая, что диагональные коэффициенты 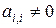 (i = 1, 2, 3,…, n), разрешим первое уравнение системы (14) относительно x1, второе – относительно x2 и т. д. В результате получим эквивалентную систему:
(i = 1, 2, 3,…, n), разрешим первое уравнение системы (14) относительно x1, второе – относительно x2 и т. д. В результате получим эквивалентную систему:
 (16)
(16)
где  при
при 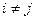
и 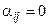 при
при 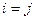 (i, j = 1, 2,…, n).
(i, j = 1, 2,…, n).
Система (16) называется системой, приведенной к нормальному виду. Введя обозначения:
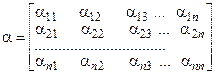 ;
; 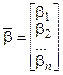 ,
,
запишем систему (16) в матричной форме:
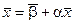 . (17)
. (17)
Решим систему (16) методом последовательных приближений. За нулевое приближение примем столбец свободных членов, т.е.  - Подставляя
- Подставляя  в правую часть системы (16) получим значения корней системы в первом приближении:
в правую часть системы (16) получим значения корней системы в первом приближении:
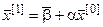
или в развернутой форме
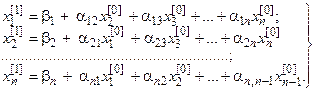 . (18)
. (18)
Подставляя полученный вектор 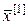 в правую часть системы (16), найдем решение этой системы в следующем, втором приближении:
в правую часть системы (16), найдем решение этой системы в следующем, втором приближении:
|
|
|
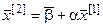
и т.д. Таким образом, любое (k +1)-е приближение вычисляют по формуле
 . (19)
. (19)
Если последовательность приближений  ,
, 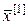 ,
, 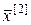 ,…,
,…, 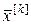 имеет предел
имеет предел 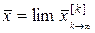 , то этот предел является решением системы (16). Действительно, переходя к пределу в уравнении (19), будем иметь
, то этот предел является решением системы (16). Действительно, переходя к пределу в уравнении (19), будем иметь

или 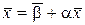 , т.е. предельный вектор
, т.е. предельный вектор 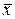 является решением системы (16), а следовательно, и системы (14) в силу их эквивалентности.
является решением системы (16), а следовательно, и системы (14) в силу их эквивалентности.
Пример 1. Методом итерации решить систему
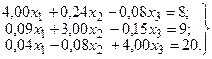 . (20)
. (20)
Приведем эту систему к нормальному виду, т.е. разрешим первое уравнение относительно x1, второе – относительно x2, третье – относительно x3:
 . (21)
. (21)
Строим последовательные приближения. За нулевое приближение принимаем: 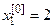 ;
;  ;
;  . Подставляя эти значения в правые части уравнений (21), получим значения искомых корней в первом приближении:
. Подставляя эти значения в правые части уравнений (21), получим значения искомых корней в первом приближении:
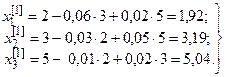 .
.
Подставляя эти найденные приближения в правую часть системы (21) получим вторые приближения корней:
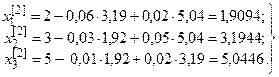 .
.
После новой подстановки найдем третьи приближения корней:
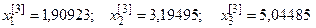 .
.
Замечания.
1. При применении метода итерации необходимо учитывать что итерационный процесс обладает свойством сходимости только при выполнении определенных условий, а именно: если для приведенной системы (16) сумма модулей элементов строк или сумма модулей элементов столбцов матрицы α меньше единицы, т.е.
|
|
|

или
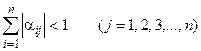 ,
,
то процесс итерации (19) сходится к единственному решению этой системы, независимо от выбора начального приближения.
Для исходной системы (14) эти условия сходимости формулируются следующим образом: если модули диагональных коэффициентов для каждого уравнения системы
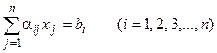
больше суммы модулей всех остальных коэффициентов (не считая свободных членов), т.е. выполнены неравенства
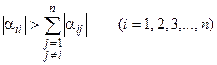
или модули диагональных коэффициентов для каждого столбца превышают сумму модулей недиагональных элементов этого столбца
 ,
,
то процесс итерации сходится.
2. Поскольку процесс итерации заканчивают на каком-то k-м шаге, то возникает естественный вопрос, какова точность найденного решения. Запишем одну из оценок погрешности решения 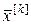 найденного на k-й итерации.
найденного на k-й итерации.
Если на k-й итерации будет обнаружено, что для каждого xi -го корня соблюдается условие
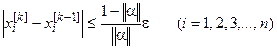 ,
,
то найденное решение 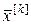 отличается от точного
отличается от точного 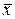 на величину не превышающую ε, т. е.
на величину не превышающую ε, т. е.
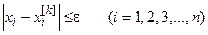 .
.
|
|
|
При этом предполагается, что последовательные приближения 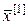 ,
, 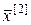 ,
, 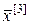 ,…,
,…, 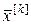 вычисляются точно, т. е. в полностью отсутствуют погрешности округлений.
вычисляются точно, т. е. в полностью отсутствуют погрешности округлений.
В приведенном условии 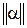 - одна из трех норм матрицы α коэффициентов системы (16)
- одна из трех норм матрицы α коэффициентов системы (16)
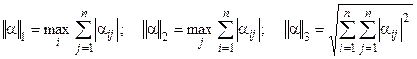 .
.
Условие сходимости метода итерации накладывает жесткие условия на коэффициенты решаемой системы уравнений
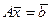 .
.
Однако, если detA ≠ 0, то с помощью элементарных преобразований исходную систему всегда можно привести к такой эквивалентной системе, для которой условия сходимости будут выполнены.
Пример 2. Систему линейных уравнений
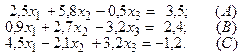
привести к эквивалентной системе, удовлетворяющей условиям сходимости метода итерации.
Из заданной системы выделяем уравнения с коэффициентами модули которых больше суммы модулей остальных коэффициентов этих уравнений. Каждое выделенное уравнение вписываем в такую строку новой системы, чтобы наибольший по модулю коэффициент оказался диагональным.
В исходной системе в уравнении (A) коэффициент при x2 по модулю больше суммы модулей остальных коэффициентов. Принимаем уравнение (A) за второе уравнение новой системы:
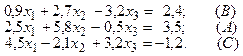
Из оставшихся неиспользованных уравнений системы составляем линейно не зависимые между собой комбинации. Так, за первое уравнение новой системы можно взять линейную комбинацию (А) + (С), т.е.
|
|
|
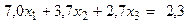 .
.
За третье уравнение можно принять линейную комбинацию (А) - 2·(B)
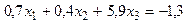 .
.
В итоге получаем преобразованную систему линейных уравнений:
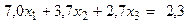 ;
;
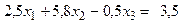 ;
;
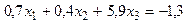
эквивалентную исходной и удовлетворяющую условиям сходимости итерационного процесса.
Метод Зейделя. Является модификацией метода итерации. Идея его состоит в том, что в вычислениях (k+1)-го приближения неизвестной xi участвуют уже вычисленные ранее (k+1)-е приближения неизвестных x1, x2,…, xi-1.
Пусть дана линейная система, приведенная к нормальному виду:
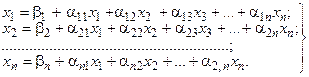 (22)
(22)
Как и в методе итерации, выберем произвольно значения 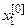 ,
, 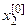 ,
,  ,…,
,…, 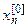 в качестве нулевого приближения для искомых корней и подставим их в первое уравнение системы (22):
в качестве нулевого приближения для искомых корней и подставим их в первое уравнение системы (22):
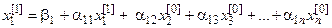 .
.
Полученное первое приближение 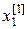 подставляем во второе уравнение системы (22):
подставляем во второе уравнение системы (22):
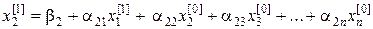 .
.
Полученные в первом приближении значения 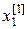 и
и 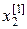 и подставляем в третье уравнение системы (22):
и подставляем в третье уравнение системы (22):

и т. д. Наконец
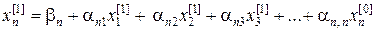 .
.
Аналогично поступаем во второй, третьей и т.д. итерациях. Таким образом, для любого (k+1)-го приближения значения искомых корней вычисляются по формулам
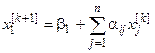 ;
;
 ;
;
……………………………………;
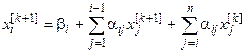 ;
;
…………………………………….;
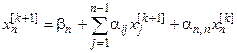 ,
,
где k = 0, 1, 2, …
Итерационный процесс продолжают до тех пор, пока для любого i-го корня не будет выполняться условие
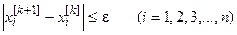 .
.
где ε - заданная точность вычисления корней системы (22).
Для метода Зейделя справедливы те же условия сходимости, что и для метода итерации. Блок схема реализации метода Зейделя решения системы линейных алгебраических уравнений приведена на рисунке 4.
Дата добавления: 2019-01-14; просмотров: 603; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
