Теоретический материал и методические указания к выполнению заданий
Число А называется пределом функции f(x) при x→a, если для любого ε>0 можно указать такое δ>0, что для любого x ≠ a, удовлетворяющего неравенству 0<|x-a|<δ, выполнялось неравенство |f(x)-A|<ε. В этом случае пишут 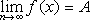 .
.
Теоремы о пределах
Теорема 1. Если существуют пределы функций f(x) и g(x) при x→a, то существует также и предел их суммы, равный сумме пределов функций f(x) и g(x):
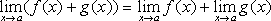
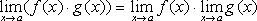

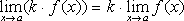
Примеры:
1) Найти предел функции 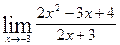
Подставим вместо x значение -3 и подсчитаем дроби
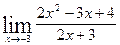 =
= 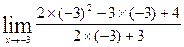 =
= 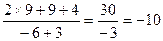
2) Найти предел функции 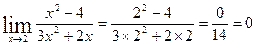
При вычислении пределов используют равенства
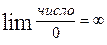
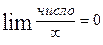

3) 
4) 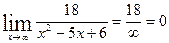
Раскрытие неопределенности вида 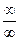
Правило: Чтобы избавиться от неопределенности вида 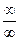 , надо числитель и знаменатель дроби разделить на x в наибольшей степени.
, надо числитель и знаменатель дроби разделить на x в наибольшей степени.
5) 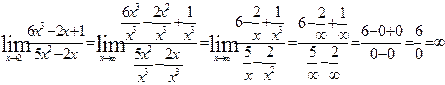
6) 
Раскрытие неопределенности вида 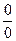
Правило: Чтобы избавиться от неопределенности вида 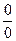 , надо числитель и знаменатель дроби разложить на множители и дробь сократить.
, надо числитель и знаменатель дроби разложить на множители и дробь сократить.
Методы разложения на множители:
1) Вынесение за скобки общего множителя.
Пример : 3x -6x =3x(x-2)
2) Формулы сокращенного умножения:
а) 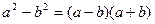
б) 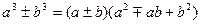
в) 
Пример 1: 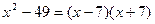
Пример 2: 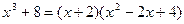
Пример 3: 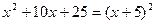
3) Разложение на множители квадратного трехчлена:
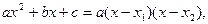 где
где 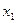 и
и  - корни квадратного трехчлена.
- корни квадратного трехчлена.
Пример:
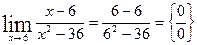
Имеет неопределенность вида 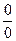 . Разложим знаменатель на множители:
. Разложим знаменатель на множители:
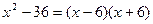
Получим:
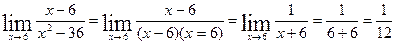
7) Найти предел
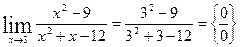
Имеет неопределенность вида 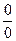 . Разложим на множители числитель:
. Разложим на множители числитель:
|
|
|
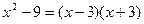
Разложим на множитель знаменатель:
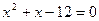
 ;
; 
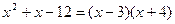
Получим:
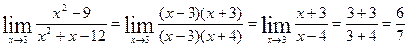
Первый и второй замечательные пределы
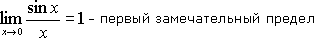

Число e – иррациональное, e≈2,7182…
Примеры:
Вычислить пределы функций при помощи первого и второго замечательного предела.
1) 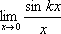
Решение
Произведем подстановку kx = y. Отсюда следует, что y→0 при x→0, а x = y/k. Тогда получим

2) 
Решение
Разделим числитель и знаменатель дроби на х (это можно сделать, т.к. x→0,а x≠0), затем воспользоваться результатом предыдущего примера:

3) 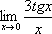
Решение
Заменив tgx = sinx/cosx, получим
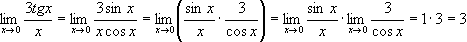
Найти предел
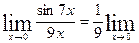
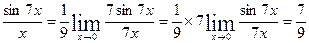

Т.к. 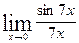 при
при 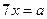 имеет вид
имеет вид  и по формуле первого замечательного
и по формуле первого замечательного
предела равен 1.
5) Найти предел 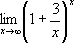
Решение
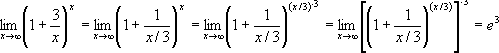
6) Найти предел 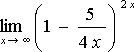
Решение
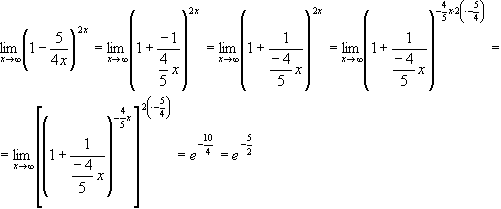
6) Найти предел 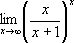
Решение
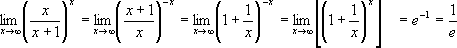
Найти предел
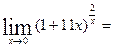
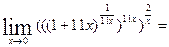 ((
(( 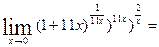
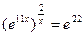
Найти предел
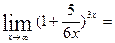 ((
(( 
Задания для самостоятельной работы
1. 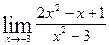 , , 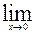 (1+ (1+ 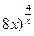
| 2. 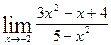 , , 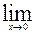 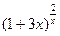
|
3. 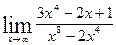 , , 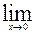 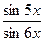
| 4. 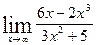 , , 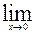 
|
5. 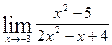 , , 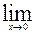 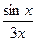
| 6. 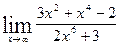 , , 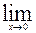  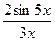
|
7. 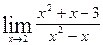 , , 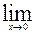 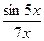
| 8. 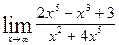 , , 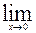 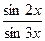
|
9. 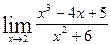 , , 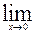 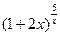
| 10. 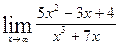 , , 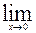 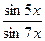
|
11. 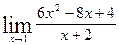 , , 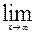 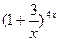
| 12. 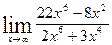 , , 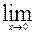 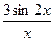
|
13.  , , 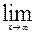 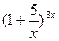
| 14. 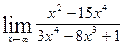 , , 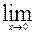 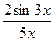
|
15. 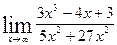 , , 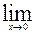 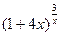
| 16.  , , 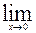 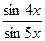
|
17.  , , 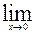 (1+ (1+ 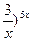
| 18. 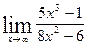 , , 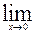 (1+9x) (1+9x) 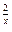
|
19. 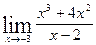 , , 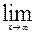 (1+ (1+ 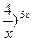
| 20. 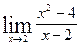 , , 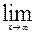 (1+ (1+ 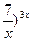
|
21.  , , 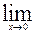 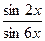
| 22. 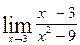 , , 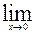 (1+ (1+ 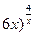
|
23. 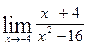 , , 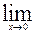 (1+7x) (1+7x) 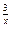
| 24. 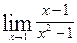 , , 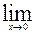  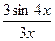
|
25. 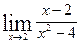 , , 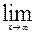 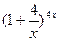
| 26.  , , 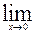 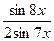
|
27. 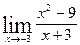 , , 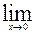 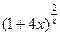
| 28.  , , 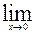 (1+7x) (1+7x) 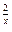
|
29.  , , 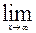 (1+ (1+ 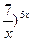
| 30. 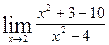 , , 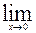 
|
31.  , , 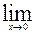 
| 32. 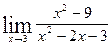 , ,  (1+ (1+ 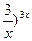
|
Раздел 3. Теория вероятностей и математическая статистика
|
|
|
Самостоятельная работа №1Индивидуальные проектные задания
- Математическая статистика и ее роль в различных сферах деятельности
- Применение теории вероятностей в повседневной жизни
Цель: получить представление об истории развития теории вероятностей, ее применении в профессии
Самостоятельная работа: работа с литературой, интернет-ресурсами.
Форма контроля: сообщение на уроке
Самостоятельная работа №2
Задачи математической статистики
В математической статистике рассматриваются две основные задачи.
Первая задача состоит в том, чтобы указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате поставленных экспериментов.
Вторая задача состоит в разработке методов анализа статистических данных в зависимости от целей исследования. К ним относятся:
1) оценка неизвестной вероятности события; оценка параметров распределения, вид которого не известен; оценка зависимости случайной величины от одной или нескольких случайных величин;
2) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого не известен.
|
|
|
Современная математическая статистика разрабатывает способы нахождения числа необходимых испытаний до начала исследования (планирование эксперимента) и решает многие другие задачи; ее определяют как науку о принятии решений в условиях неопределенности.
Итак, основная задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
В основе задач, решаемых методами математической статистики, лежит необходимость изучения совокупности однородных объектов, относительно некоторого качественного или количественного признака.
Например, при изучении партии однородных товаров, хранящихся на базе, качественным признаком могут служить сортовые, а количественным — весовые характеристики, изменяющиеся в процессе хранения.
Совокупность всех объектов, подчиненных данному признаку, называют генеральной совокупностью, а число таких объектов — объемом генеральной совокупности.
На практике, как правило, обследование всех объектов генеральной совокупности не производится в силу излишней трудоемкости такого процесса. Обычно из всей совокупности отбирают ограниченное число объектов, которые и подвергают изучению. Такую случайно отобранную совокупность называют выборочной совокупностью, или выборкой. Для того чтобы по данным выборки достаточно уверенно характеризовать всю генеральную совокупность, необходимо, чтобы отобранные элементы правильно ее представляли.
|
|
|
Определение: Выборку, достаточно хорошо описывающую всю генеральную совокупность, называют репрезентативной (представительной).
Для получения репрезентативной выборки необходимо, чтобы все отобранные элементы имели одинаковую вероятность попасть в выборку. В случае большого объема N генеральной совокупности, хорошие результаты в этом смысле дает использование таблицы «случайных чисел».
Для того чтобы отобрать, например, 20 объектов из пронумерованной генеральной совокупности, можно открыть любую страницу таблицы «случайных чисел» и выписать подряд 20 случайных чисел. В выборку включают те объекты, номера которых совпали с выписанными случайными числами (случайные числа, превышающие N , при выписывании пропускаются).
Определение:| Элементы х1 х2, ..., х n , попавшие в выборку, называют вариантами, а их количество п — объемом выборки.
Отобранные элементы располагают обычно в порядке их возрастании: х(|) <= х(2) <= ... <= х(n). Такая последовательность вариант называется вариационным рядом. Разность между максимальным и минимальным элементами выборки Z = х(п) - хт называют размахом выборки.
Среди п элементов выборки могут встречаться повторяющиеся. Если, например, элемент х1 встречается n 1 раз, х2 - п2 раз, ..., хк – пк раз, то числа п1 п2,..., пк называются частотами вариант х1 х2,..., хк. Очевидно, что сумма всех частот равна объему выборки, т. е. п1 + n 2 + ... + пк = п, или Σni = п.
Расположенная в порядке возрастания вариант последовательность пар чисел, составленная из вариант и их частот (х1 n1), (х2, п2), …, (хк, пк), называется статистическим рядом, или статистическим распределением.
При этом пользуются табличной записью:
| Xi | x1 | х2 | ... | хк |
| ni | n 1 | п2 | пк |
Очевидно, что сумма частот всех элементов выборки равна единице:

Пример 1. Записать вариационный ряд и статистическое распределение элементов выборки 5, 0, 3, 7, 0, 10, 5, 0, 5, 2, 10, 2, 0, 7, 2, 0, 4, 7, 7, 4 из числа рабочих дней в году, пропущенных по болезни работниками ПОП. Определить размах выборки.
Решение. Объем выборки п = 20. Упорядочив элементы выборки по величине, получим вариационный ряд 0, 0, 0, 0, 0, 2, 2, 2, 3, 4, 4, 5, 5, 5, 7, 7, 7, 7, 10, 10 (размах выборки z = 10 - 0 = 10):
| Xi | 0 | 2 | 3 | 4 | 5 | 7 | 10 |
| ni | 5 | 3 | 1 | 2 | 3 | 4 | 2 |
При большом объеме выборки для упрощения вычислений, ее элементы объединяют в группы (разряды), представляя выборку в виде группированного статистического ряда (распределения). Для этого интервал, содержащий все элементы, разбивают на к непересекающихся интервалов. Вычисления значительно упрощаются, если этиинтервалы имеют одинаковую длину h = 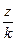 . После того, как интервалы выбраны, определяются частоты — количество элементов п i * выборки, попавших в i-й интервал, а сами элементы, попавшие в этот интервал, считаются равными его середине х i * (элемент, совпадающий с верхней границей интервала, относится к последующему интервалу).
. После того, как интервалы выбраны, определяются частоты — количество элементов п i * выборки, попавших в i-й интервал, а сами элементы, попавшие в этот интервал, считаются равными его середине х i * (элемент, совпадающий с верхней границей интервала, относится к последующему интервалу).
Число интервалов k группировки берется в зависимости от объема выборки. При этом следует помнить, что группировка выборки вносит погрешности в дальнейшие вычисления. Эти погрешности растут с уменьшением числа интервалов. В процессе составления группированного статистического распределения подсчитываются также нако пленные частоты 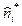
 п* (накопленная частота i-го интервала равна сумме частот самого i-го и всех предыдущих интервалов, т. е.
п* (накопленная частота i-го интервала равна сумме частот самого i-го и всех предыдущих интервалов, т. е. 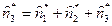 ), относительные частоты
), относительные частоты  —- и накопленные частоты
—- и накопленные частоты  -
-
Пример 2. Известно время недельной загрузки электрических духовых шкафов 50 обследованных предприятий общественного питания в часах:
38 60 41 51 33 42 45 21 53 60
61 35 47 72 41 45 44 56 30 40
60 52 47 46 49 49 14 57 54 59
67 65 39 48 43 60 54 42 59 50
77 47 28 48 58 32 42 58 61 30
Найти размах выборки, число и длину интервалов, а также составить таблицу частот (записать группированное статистическое распределение). Первый интервал взять 14- 23.
Решение. Будем проводить группировку по интервалам равной длины h = 23 –– 14 = 9. Размах выборки z = 77 - 14 = 63. Тогда необходимое число интервалов к = 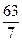 = 7. Результаты группировки сведены в таблицу
= 7. Результаты группировки сведены в таблицу
| Номер интервала i | Границы интервала | Середина интервала х i * | Частота
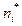
| Относительная частота 
| Накопленная относительная частота 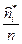
|
| 1 | 14-23 | 18,5 | 2 | 0,04 | 0,04 |
| 2 | 23-32 | 27,5 | 3 | 0,06 | 0,Ю |
| 3 | 32-41 | 36,5 | 6 | 0,12 | 0,22 |
| 4 | 41-50 | 45,5 | 17 | 0,34 | 0,56 |
| 5 | 50-59 | 54,5 | 10 | 0,20 | 0,76 |
| 6 | 59-68 | 63,5 | 9 | 0,18 | 0,94 |
| 7 | 68-77 | 72,5 | 8 | 0,16 | 1,00 |
В целях наглядности строят различные графики статистического распределения. Они помогают лучше представить себе характер распределения элементов выборки, а иногда и сделать предварительные предположения о законе распределения генеральной совокупности.
Такими графиками являются полигон частот и гистограммы.
Полигоном частот называют ломаную линию, вершинами которой являются точки (х1 n1), (х2, п2), …, (хк, пк), определяемые элементами статистического ряда.
Для его построения на оси абсцисс откладываются варианты xi а по оси ординат — соответствующие им частоты ni . Построенные точки ( xi ni ) соединяются отрезками прямых и получается полигон частот (для группированной выборки полигон частот строится по точкам (xi * ,п i *)).
Для группированной выборки обычно строится гистограмма частот.
Гистограммой частот называют ступенчатую фигуру, составленную из прямоугольников, построенных на интервалах так, что площадь каждого прямоугольника численно равна частоте п i * варианты xi * , расположенной в середине i-го интервала.
Отсюда следует, что площадь гистограммы частот равна объему выборки п. При равных длинах интервалов разбиения п, высоты прямоугольников равны 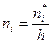
Пример: Построить полигон и гистограмму частот и относительных частот по группированной выборке примера
Решение. По результатам группировки (см. таблицу из примера 2) строим соответственно полигон частот (рис. а), гистограмму частот (рисб). 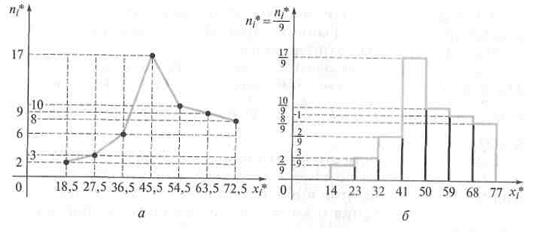
Определение: Модой (Мо) называют варианту выборки, имеющую наибольшую частоту
Пример: По данным статистического распределения выборки найти моду Мо
| xi | 1 | 3 | 5 | 7 | 9 |
| ni | 1 | 5 | 6 | 5 | 3 |
Решение: Поскольку наибольшая частота выборки n3=6 принадлежит элементу x3 = 5 , то мода равна Мо=5.
Определение: Медианой (Ме) называют варианту выборки, делящую вариационный ряд на две части, равные по числу вариант.
При этом, если объем выборки – число нечетное, то медианой будет являться средний элемент вариационного ряда; если же объем выборки – число четное, то медианой будет величина, равная полусумме двух вариант выборки, расположенных в середине вариационного ряда т.е. 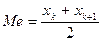 .
.
Пример: По данным вариационных рядов определить медиану:
1) 2, 3, 6, 7, 9 2) 2, 3, 5, 7; в) 2, 2, 3, 5, 7, 7, 8, 9, 9, 11
Решение:
1) Объем выборки n=5 – нечетное число, следовательно, медианой будет средний элемент, т.е. Ме = 6;
2) Объем выборки n=4 – четное число, следовательно, медианой будет полусумма двух средних значений: 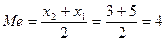
3) Объем выборки n=4 – четное число, следовательно, Ме=7
Дата добавления: 2019-01-14; просмотров: 458; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
