Решения задач районной олимпиады по математике 2015 г.
Класс
7.1. Для приготовления 1 кг мороженного требуется воды в 2,5 раза больше, чем сливок, а сахара на 0,1 кг больше, чем сливок. Сколько требуется сливок, воды и сахара?
♦ 0,2 сливок, 0,5 воды, 0,3 сахара.
7.2. Найдите наименьшее пятизначное натуральное число, все цифры которого различны, и которое делится на 71 без остатка.
♦ Ответ: 10295. Ищем число возле самого маленького пятизначного числа из пяти различных цифр – это 10234, потому что первой значащей цифрой не может быть 0, а поэтому число начинается с 1. А затем выписывали самое маленькое из возможных. Часть таблицы умножения на 71 выглядит так:

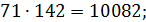
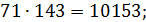
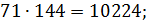
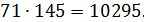
7.3. Дети ходили в лес по грибы. Если Аня отдаст половину своих грибов Вите, то у всех детей станет поровну грибов. А если вместо этого Аня отдаст все свои грибы Саше, то у Саши станет столько грибов, сколько у всех остальных вместе взятых. Сколько детей ходило за грибами?
♦ Ответ: 6. Если у Ани 2х грибов, то после того, как она отдаст половину Вите, то у всех детей станет по х грибов. Стало быть у Вити изначально грибов не было. Если Аня отдаст все свои грибы Саше, то у Саши их станет 3х, то есть в лес ходили ещё три человека. За грибами ходили 6 человек.
7.4. Стороны 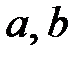 и
и 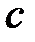 треугольника относятся как
треугольника относятся как 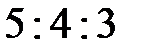 . Периметр треугольника 48 см. Найдите сумму
. Периметр треугольника 48 см. Найдите сумму 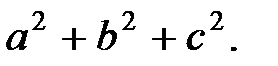
♦ Длины сторон 20, 16 и 12; 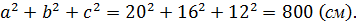
7.5. Костяшка домино имеет размеры 3 × 5 × 1 (см). Определите максимальное количество костяшек домино, которое можно поместить в коробку размером 11 × 14 × 1 (см).
|
|
|
♦ Ответ: 10. Так как 14 = 3 + 3 +3 + 5, а 11 = 3 + 3 + 5, то 5 костяшек укладываются с одной стороны и 5 симметрично. Очевидно, что 11 костяшек не укладываются.
Класс
8.1. Существуют ли натуральные числа a, b и c, для которых сумма 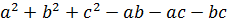 равна 21?
равна 21?
♦ Да. Например, при 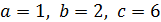 получаем
получаем 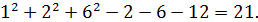
Удалось подобрать так: первые два числа взяли произвольно. Получили 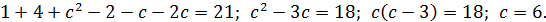
8.2. В трапеции 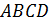 длины оснований известны
длины оснований известны 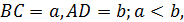 F – середина большего основания
F – середина большего основания 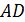 , M –точка пересечения BF и AC; N – точка пересечения CF и BD. Докажите, что треугольники
, M –точка пересечения BF и AC; N – точка пересечения CF и BD. Докажите, что треугольники 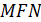 и
и 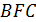 подобны.
подобны.
♦ Из подобия треугольников 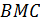 и
и 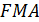 имеем
имеем

Из подобия треугольников  и
и 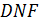 имеем
имеем
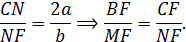
Треугольники подобны по двум сторонам и углу между ними.
8.3. Костяшка домино имеет размеры 3 × 5 × 1 (см). Определите максимальное количество костяшек домино, которое можно поместить в коробку размером 12 × 13 × 3 (см).
♦ Достаточно описать укладку 30 костяшек, чтобы считать задачу решённой.
8.4. Задание олимпиады состоит из 20 задач. За каждую правильно решённую задачу жюри ставит 8 баллов, за каждую неверно решённую задачу – минус 5 баллов. Если же ученик не решал задачи, то за неё ему ставят 0 баллов. В результате Герман получил 13 баллов. Сколько задач он решал?
|
|
|
♦ Ответ: 13. Пусть х – количество правильно решённых задач, у – неправильно. Тогда
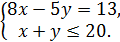
Перепишем первое уравнение так:

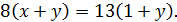
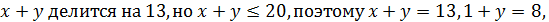
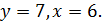
8.5. Пусть 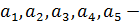 целые числа, а
целые числа, а 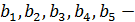 те же числа, но взятые в другом порядке. Докажите, что число
те же числа, но взятые в другом порядке. Докажите, что число
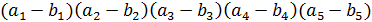
является чётным.
♦ Предположим противное, что число нечётное. Но тогда все сомножители нечётные, и их сумма нечётная, но на самом деле сумма чётная
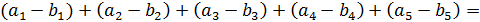
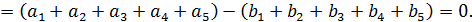
Не забудьте, что 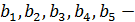 те же числа, но взятые в другом порядке, поэтому суммы
те же числа, но взятые в другом порядке, поэтому суммы 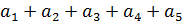 и
и 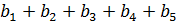 равны. Полученное противоречие говорит о том, что наше предположение неверное.
равны. Полученное противоречие говорит о том, что наше предположение неверное.
Класс
9.1. Существуют ли натуральные числа a, b и c, для которых сумма 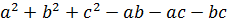 равна 54?
равна 54?
♦ Ответ: Нет. Все три числа чётными не могут быть, так как в этом случае сумма делится на 4, а 54 на 4 не делится. Если 2 чётных, а одно нечётно, то сумма нечётна, а 54 – число чётное. И такое случай невозможен. По этой же причине невозможен случай, когда одно чётно, а два нечётны. Остался случай, когда все три числа нечётны
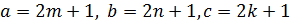 .
.
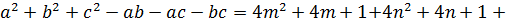
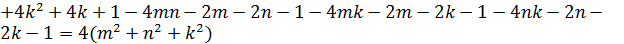 .
.
Сумма делится на 4. И в этом случае получаем противоречие с тем, что 54 на 4 не делится.
9.2. В трапеции 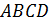 длины оснований известны
длины оснований известны 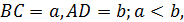 F – середина большего основания
F – середина большего основания 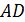 , M –точка пересечения BF и AC; N – точка пересечения CF и BD. Докажите, что прямая MN параллельна основанию.
, M –точка пересечения BF и AC; N – точка пересечения CF и BD. Докажите, что прямая MN параллельна основанию.
|
|
|
♦ Из подобия треугольников 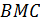 и
и 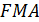 имеем
имеем

Из подобия треугольников  и
и 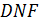 имеем
имеем
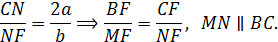
Треугольники подобны по двум сторонам и углу между ними.
9. 3. Решите систему
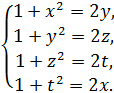
♦ Ответ: (1; 1; 1). Сложив все уравнения и перегруппировав слагаемые, получим
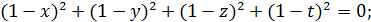
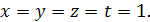
9.4. При каких значениях a система имеет решения
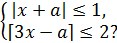
♦ Ответ: 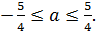
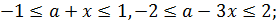
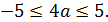
Но эти неравенства – только следствия исходной системы. Поэтому надо проверить, что a действительно может принимать все эти значения.
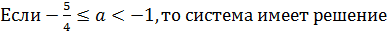
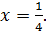
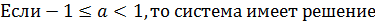
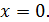
Если 
9.5. На карте обозначены 4 деревни A, B, C и D. Деревня А соединена тропинками с деревнями В и D. Деревня С соединена тропинками с деревнями В и D. Деревни В и D также соединяет тропинка. В справочнике написано, что на маршруте АВС и BCD по 10 колдобин. На маршруте ABD – 22 колдобины. На маршруте ADB – 45 колдобин. Туристы хотят добраться из А в D так, чтобы на их пути было как можно меньше колдобин. По какому маршруту им надо идти? Обязательно докажите,что на указанном Вами маршруте действительно меньше всего колдобин.
♦ Ответ:ABCD .Есть всего три пути, не проходящих по одной тропинке дважды AD, ABD и ABCD. На ABD 22 колдобины, поэтому на BD их не более 22. На ADB 45 колдобин, при этом на BD не более 22, следовательно, на AD – не менее 23. На АВС и BCD по 10 колдобин, следовательно, на ABCD – не более 20. Итак, на ABCD меньше колдобин, чем на AD или ABD.
|
|
|
Решения 10 класс
10.1. Все коэффициенты квадратного трёхчлена – нечётные целые числа. Докажите, что у него нет корней вида  , где n – натуральное число.
, где n – натуральное число.
♦ Пусть a, b и c – нечётные целые числа и
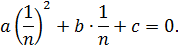
Освободимся от знаменателя:
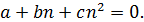
Если n нечётно, слева сумма трёх нечётных чисел, т. е. нечётное число, а справа – чётное число. Противоречие. Если чётно, то слева первое слагаемое нечётно, а два других слагаемых чётны, т. е. опять сумма нечётна.
10.2. В трапеции 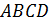 длины оснований известны
длины оснований известны 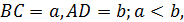 F – середина большего основания AD, M –точка пересечения BF и AC; N – точка пересечения CF и BD. Найдите длину отрезка MN.
F – середина большего основания AD, M –точка пересечения BF и AC; N – точка пересечения CF и BD. Найдите длину отрезка MN.
♦ Ответ: 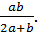
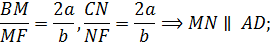
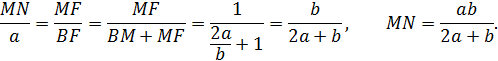
10. 3. Решите систему
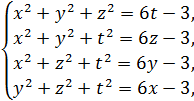
♦ Ответ: (1; 1; 1; 1). Сложив почленно все уравнения системы, получим


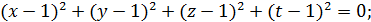
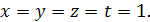
10.4. Одуванчик утром распускается, три дня цветёт жёлтым, на четвёртый день утром становится белым, а к вечеру пятого дня облетает. В понедельник днём на поляне было 20 желтых и 14 белых одуванчиков, а в среду – 15 жёлтых и 11 белых. Сколько белых одуванчиков будет на поляне в субботу?
♦ Ответ: 6. Распустившийся одуванчик бывает белым на четвертый и пятый день. В субботу будут белыми те одуванчики, которые распустились во вторник или среду. Определим, сколько их.14 одуванчиков, которые были белыми в понедельник, к среде облетели, а 20 жёлтых заведомо дожили до среды (быть может, став белыми). В среду на поляне было 15 + 11 = 26 одуванчиков. из них 20 были на поляне ещё в понедельник, а остальные 6 как раз распустились во вторник и среду.
10.5. При каких значениях параметра 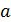 система имеет единственное решение
система имеет единственное решение
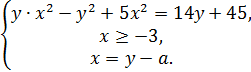
♦ Ответ: система имеет единственное решение при 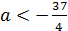 или при
или при  .
.
Решение 1. Запишем первое уравнение в виде
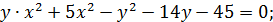
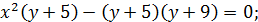
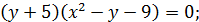
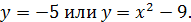
Построим графики этих функций. Изменяя 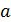 , будем перемещать прямую
, будем перемещать прямую 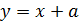 параллельно прямой
параллельно прямой 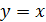 . Тогда в области
. Тогда в области 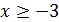 эта прямая с графиками взятых функций имеет единственную общюю точку при
эта прямая с графиками взятых функций имеет единственную общюю точку при 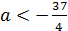 или при
или при  . В остальных случаях значений
. В остальных случаях значений 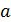 общих точек две или три.
общих точек две или три.
Решение 2. Запишем первое уравнение в виде
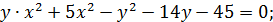
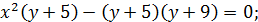
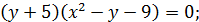
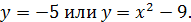
В случае 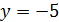 имеем
имеем 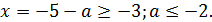 При
При 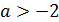 решений системы нет. При
решений системы нет. При 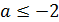 система имеет одно решение
система имеет одно решение 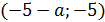 .
.
При 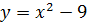 уравнение
уравнение 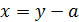 принимает вид
принимает вид
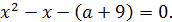
Дискриминант полученного квадратного уравнения равен
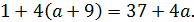
Отсюда, это уравнение не имеет корней при 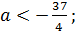 имеет единственный корень при
имеет единственный корень при 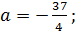 имеет два корня при
имеет два корня при 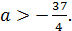
Квадратичная функция  достигает минимума при
достигает минимума при 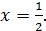 При
При  получим
получим 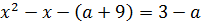 Таким образом, при
Таким образом, при  только один корень из двух удовлетворяет условию
только один корень из двух удовлетворяет условию 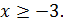
Определим значения 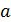 , при которых возможны совпадения решений из первого и второго случаев:
, при которых возможны совпадения решений из первого и второго случаев:

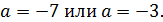
Таким образом, исходная система имеет единственное решение при
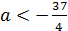 или при
или при  .
.
Класс
11.1. Все коэффициенты квадратного трёхчлена – нечётные целые числа. Докажите, что у него нет рациональных корней.
♦ Пусть a, b и c – нечётные целые числа и
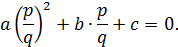
Освободимся от знаменателя:
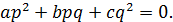
Если p и q нечётны, то слева сумма трёх нечётных чисел, т. е. нечётное число, а справа – чётное число. Противоречие. Если одно из них чётно, а другое нечётно, то слева одно слагаемое нечётно, а два других слагаемых чётны, т. е. опять сумма нечётна.
11.2. Длины оснований трапеции 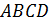 известны:
известны: 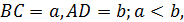 F – середина большего основания AD, M –точка пересечения BF и AC; N – точка пересечения CF и BD. Найдите длину отрезка, высекаемого на прямой MN боковыми сторонами трапеции.
F – середина большего основания AD, M –точка пересечения BF и AC; N – точка пересечения CF и BD. Найдите длину отрезка, высекаемого на прямой MN боковыми сторонами трапеции.
♦ Ответ: 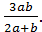
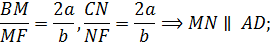
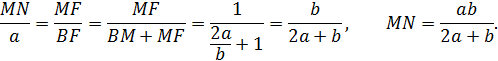
Пусть L – точка пересечения прямых MN и AB, а K – точка пересечения прямых MN и CD. Аналогично проделанным вычислениям получим, что
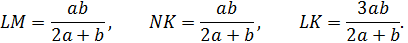
Ответ:  .
.
11.3. Два миллиона отмеченных точек целиком расположены внутри окружности диаметра 1 см. Существует ли прямая, по каждую сторону от которой находилось бы ровно по одному миллиону отмеченных точек? Просто ответ "Да" или "Нет" без обоснования не является решением задачи.
♦ Ответ: да. Через каждую пару отмеченных точек проведём прямые. Возьмём точку вне данного круга, не лежащую ни на одной из этих прямых. Проведём через эту точку прямую, проходящую вне окружности. Проворачиваем эту прямую вокруг данной точки. При этом движении прямая последовательно проходит через отмеченные точки. Она не сможет проходить одновременно более, чем через одну точку, так эти прямые уже проведены. Следовательно, повернув прямую так, чтобы она последовательно прошла ровно через миллион отмеченных точек, мы получим искомую прямую.
11.4. Одуванчик утром распускается, три дня цветёт жёлтым, на четвёртый день утром становится белым, а к вечеру пятого дня облетает. В понедельник днём на поляне было 20 желтых и 14 белых одуванчиков, а в среду – 15 жёлтых и 11 белых. Сколько белых одуванчиков будет на поляне в субботу?
♦ Ответ: 6. Распустившийся одуванчик бывает белым на четвертый и пятый день. В субботу будут белыми те одуванчики, которые распустились во вторник или среду. Определим, сколько их.14 одуванчиков, которые были белыми в понедельник, к среде облетели, а 20 жёлтых заведомо дожили до среды (быть может, став белыми). В среду на поляне было 15 + 11 = 26 одуванчиков. из них 20 были на поляне ещё в понедельник, а остальные 6 как раз распустились во вторник и среду.
11.5. При каких значениях параметра 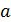 система имеет единственное решение
система имеет единственное решение
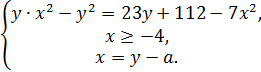
♦ Ответ: система имеет единственное решение при 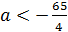 или при
или при 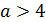 .
.
Решение 1. Запишем первое уравнение в виде
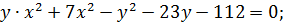
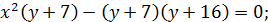
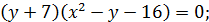
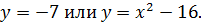
Построим графики этих функций. Изменяя 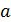 , будем перемещать прямую
, будем перемещать прямую 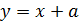 параллельно прямой
параллельно прямой 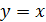 . Тогда в области
. Тогда в области 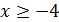 эта прямая с графиками взятых функций имеет единственную общюю точку при
эта прямая с графиками взятых функций имеет единственную общюю точку при 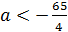 или при
или при 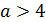 . В остальных случаях значений
. В остальных случаях значений 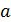 общих точек две или три.
общих точек две или три.
Решение 2. Запишем первое уравнение в виде
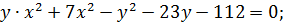
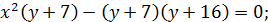
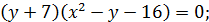
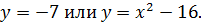
В случае 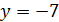 имеем
имеем 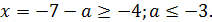 При
При 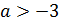 решений системы нет. При
решений системы нет. При 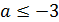 решение одно
решение одно 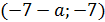 .
.
При 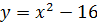 уравнение
уравнение 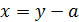 принимает вид
принимает вид
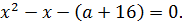
Дискриминант полученного квадратного уравнения равен
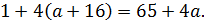
Отсюда, это уравнение не имеет корней при 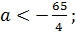 имеет единственный корень при
имеет единственный корень при 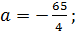 имеет два корня при
имеет два корня при 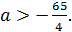
Квадратичная функция 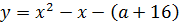 достигает минимума при
достигает минимума при 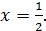 При
При 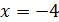 получим
получим 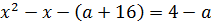 Таким образом, при
Таким образом, при 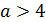 только один корень из двух удовлетворяет условию
только один корень из двух удовлетворяет условию 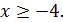
Определим значения 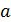 , при которых возможны совпадения решений из первого и второго случаев:
, при которых возможны совпадения решений из первого и второго случаев:
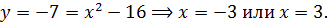

Таким образом, исходная система имеет единственное решение при
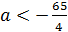 или при
или при 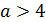 .
.
Критерии оценивания
7 баллов – Полное верное обоснованное решение
6 баллов – Верное решение, но имеются небольшие недочёты, в целом не влияющие на решение
5 баллов – Решение в целом верное. Однако оно содержит ошибки, либо пропущены случаи, не влияющие на логику рассуждений
4 балла – В том случае, когда решение делится на две равные части – решение одной части
3 балла – Доказаны вспомогательные утверждения, помогающие в решении задачи
2 балла – Рассмотрены отдельные случаи при отсутствии решения
1 балл – Решение неверное. Была попытка решения.
0 баллов – Решение отсутствует
МУНИЦИПАЛЬНЫЙ ЭТАП
Дата добавления: 2018-11-24; просмотров: 188; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
