Восстановление математических действий
Теория > Олимпиада
ВОССТАНОВЛЕНИЕ ЗНАКОВ ДЕЙСТВИЙ
Такие задания очень часто встречаются на олимпиадах. Звучат, как правило, так: «Замените каждую из звездочек знаками арифметических действий, чтобы выполнялось равенство»
Здесь нет необходимых алгоритмов действий, нужно хорошо знать азы сложения и вычитания, а также умножения и деления.
Напомним, что знаки арифметических действий это знаки сложения, вычитания, умножения, деления и возведения в степень, а также скобок и т.п.
Бывает, что у решения несколько ответов, но достаточно записать один.
Примеры восстановления знаков действий
1. В записи 1 * 2 * 3 * 4 * 5 = 100 замените каждую из звездочек знаками арифметических действий и расставьте скобки так, чтобы получилось верное равенство.
В этом примере нам будет недостаточно только знаков сложения и вычитания, нужно задействовать знак умножения..
Подойдет, например, такая расстановка: 1*(2 + 3)*4*5= 100
2. Расставьте знаки сложения и вычитания между цифрами 1 2 3 4 5 6 7 8 9 так, чтобы в результате получилось число 100.
Здесь можно предложить такой вариант: 123-4-5-6-7 + 8-9= 100.
3. Пользуясь знаками арифметических действий, запишите двумя двойками наибольшее натуральное число.
Запишем с помощью двух двоек все натуральные числа. Их немного:
2 + 2 = 4, 2-2 = 4, 2*2 = 4, 22.
Наибольшим из них является число 22. Интересно, что для его записи знаки арифметических действий вообще не понадобились.
|
|
|
4. В записи 9 9 9 9 9 9 9 9 поставьте знаки сложения и вычитания так, чтобы значение получившегося выражения было равно 1998.
999 + 999 + 9 - 9 = 1998
5. Применяя знаки арифметических действий, запишите тремя двойками числа: а) 2; в) 3.
2/2*2 = 2
2/2+2 = 3
6. Используя знаки арифметических действий и скобки, запишите число 100:
а) пятью пятерками; б) четырьмя пятерками, и) восмью пятерками
5*5*5 – (5*5) = 100
(5+5+5+5)*5 = 100
(5+5) *(5+5) = 100
(5*5)+(5*5)+(5*5)+(5*5) = 100
7. Расставьте в левой части равенства скобки и знаки арифметических действий так, чтобы выполнилось равенство:
1) 7 7 7 7 7 7 7 7 = 700
2) 6 6 6 6 6 6 6 6 6 = 600
3) 4 4 4 4 4 4 4 4 4 4 = 500
7777 / 77*7 - 7 = 700
(666-66) + 6-6+6-6 = 600
44 + 44 - 44 + 4*4 + 4*4 = 500 или 4*4 + 444 + 44+ 4 - 4 - 4 = 500
8. Используя знаки арифметических действий и скобки, запишите число 1000 восьмью восьмёрками
(8*8+8*8)*8-8-8-8 = 1000 или 888+88+8+8+8 = 1000
9. Между цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9 расставьте знаки арифметических действий и скобки так, чтобы полученное выражение имело значение 100.
1+2+3+4+5+6+7+8*9 = 100
·
Курс подготовки к олимпиадам 5-6 класс
· Математические ребусы
· Задачи на четность и нечетность
· Восстановление математических действий
· Задачи на нахождении площади
· Задачи на взвешивание
· Задачи на переливание
|
|
|
· Задачи на рыцарей и лжецов
· Делимость целых чисел и остатки
· Задачи на смеси
·
Вычисление площадей фигур, изображенных на клетчатой бумаге
Теория > Олимпиада
На олимпиадах часто бывают задания, в которых требуется вычислить площадь фигуры, изображенной на листе бумаги в клетку. Как правило, эти задания не вызывают больших проблем, если фигура представляет собой ромб или трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур.
Трудности появляются, когда фигура представляет собой некоторый произвольный многоугольник.
Изучение специальной литературы и интернет источников, показало, что существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика.
Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.
Возможны следующие случаи.
1. Фигура представляет собой треугольник:
|
|
|
Воспользуемся ФОРМУЛОЙ ПИКА
Площадь искомой фигуры можно найти по формуле:
М – количество узлов (пересечений линий) на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
S = M/2 + N - 1
Рассмотрим как работает формула на конкретном треугольнике:
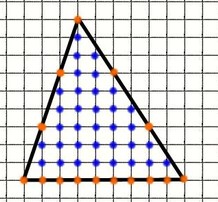В данном треугольнике мы обозначили красным цветом количество узлов на границе треугольника M = 15 (обозначены красным)
А синим цветом - количество узлов внутри треугольника
N = 34 (обозначены синим)
Масштаб : 1 клетка = 1 см
S = M/2 + N - 1 = 15 / 2 + 34 - 1 = 40, 5 см2
2. Фигура представляет собой треугольник, параллелограмм, трапецию:
здесь также можно воспользоваться формулой Пика:
S = M/2 + N - 1
Рассмотри ещё пример. Найдём площадь параллелограмма:
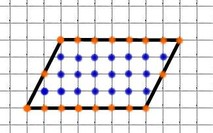В данном параллелограмме мы обозначили красным цветом количество узлов на границе треугольника M = 24 (обозначены красным)
А синим цветом - количество узлов внутри треугольника
N = 25 (обозначены синим)
Масштаб : 1 клетка = 1 см
S = M/2 + N - 1 = 24 / 2 + 25 - 1 = 36 см2
3. Фигура представляет собой многоугольник:
Если фигура представляет собой многоугольник то возможно использовать следующие методы.
Метод разбиения:
1) разбить многоугольник на треугольники, прямоугольники;
|
|
|
2) вычислить площади полученных фигур;
3) найти сумму всех площадей полученных фигур.
Метод - формула Пика
Этот метод работает и на многоугольниках. Посмотрим на примере:
В данном многоугольнике мы обозначили красным цветом количество узлов на границе треугольника M = 14 (обозначены красным)
А синим цветом - количество узлов внутри треугольника
N = 43 (обозначены синим)
Масштаб : 1 клетка = 1 см
S = M/2 + N - 1 = 14 / 2 + 43 - 1 = 49 см2
Когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.
·
Курс подготовки к олимпиадам 5-6 класс
· Математические ребусы
· Задачи на четность и нечетность
· Восстановление математических действий
· Задачи на нахождении площади
· Задачи на взвешивание
· Задачи на переливание
· Задачи на рыцарей и лжецов
· Делимость целых чисел и остатки
· Задачи на смеси
·
Задачи на взвешивание
Теория > Олимпиада
Задачи на взвешивание — тип олимпиадных задач по математике, в которых требуется у локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Чаще всего в качестве взвешиваемых объектов используются монеты. Реже имеется также набор гирек известной массы.
Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой. Задачи данного типа чаще всего решаются методом рассуждений.
При решении этих задач часто используется следующее соображение: весы могут пребывать в одном из тёх состояний
• перевесила левая чашка
• перевесила правая чашка
• чашки находятся в равновесии
Рассмотрим, как эти рассуждения применяются при решении задач
Задача 1. Имеются неправильные чашечные весы, мешок крупы и правильная гиря массой в 1 кг. Как отвесить на этих весах 1 кг крупы?
Решение. Поставим на одну чашку весов гирю весом 1 кг и уравновесим весы крупой из мешка. Чаши весов находятся в равновесии - с обоих сторон по 1 кг. Теперь снимем с весов эту гирю и вместо нее насыпем крупу. Когда этой крупы станет ровно 1 кг, весы снова окажутся в равновесии.
Задача 2. У Антошки есть 27 золотых монет. Но известно, что Филя заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Антошке определить фальшивую монету?
Решение. Разделим монеты на 3 кучки по 9 монет (27 : 3 = 9). Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка ( достаточно, чтобы весы показали равенство, чтобы сделать вывод, что фальшивка - в третьей кучке). Теперь, аналогично, разделим выбранную кучку с фальшивкой на три части по три монеты (9 : 3 = 3), положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую: кладем на чаши весов по 1 монете - фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части. Задача решена.
Задача 3. Имеются чашечные весы без гирь и 4 одинаковые по внешнему облику монеты. Одна из монет фальшивка, кроме того масса монеты по отношению к другим монетам неизвестна. Но все настоящие монеты одного веса. Сколько надо взвешиваний, чтобы определить фальшивую монету?
Решение. Если у нас 3 монеты, достаточно двух взвешиваний. Кладём на каждую чашку весов по одной монете. Если весы не в равновесии, значит, та монета, которая осталась, — настоящая. Кладём её на весы с любой из остальных и сразу определяем, какая из них фальшивка. Если же весы в равновесии, значит, фальшивая монета та, которая осталась, и вторым взвешиванием можно даже определить, легче она или тяжелее, чем настоящие. Если у нас 4 монеты, опять достаточно двух взвешиваний. Разделим наши монеты на две кучки по 2 монеты и положим одну из кучек на весы — по монете на каждую чашку. Если весы в равновесии, то следовательно обе монеты на них настоящие. Если весы не в равновесии, то обе монеты на столе настоящие. Итак, теперь мы знаем, в какой кучке лежит фальшивая монета. Положим на одну чашку весов монету из кучки, где обе настоящие, на вторую — монету из кучки, где фальшивая. Если при этом весы будут в равновесии, значит, фальшивая монета осталась на столе, а если не в равновесии, значит, мы положили её на весы (в этом случае мы даже узнаем, легче она или тяжелее).
Задача 4. В корзине лежат 13 яблок. Имеются весы, с помощью которых можно узнать суммарный вес любых двух яблок. Придумайте способ выяснить за 8 взвешиваний суммарный вес всех яблок.
Решение. Занумеруем яблоки. Взвесим первое яблоко со вторым, второе с третьим и третье с первым, затем сложим полученные веса и получим удвоенный вес трех яблок, а затем и вес трех яблок, следовательно, за три взвешивания мы узнали суммарный вес первых трех яблок. Осталось пять взвешиваний и десять яблок, которые взвешиваем попарно и, суммируя все данные, получим вес 13 яблок.
·
Курс подготовки к олимпиадам 5-6 класс
· Математические ребусы
· Задачи на четность и нечетность
· Восстановление математических действий
· Задачи на нахождении площади
· Задачи на взвешивание
· Задачи на переливание
· Задачи на рыцарей и лжецов
· Делимость целых чисел и остатки
· Задачи на смеси
·
Задачи на переливание
Теория > Олимпиада
Задачи на переливание - это задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости. Простейший прием решения задач этого класса состоит в переборе возможных вариантов.
В задачах на переливания требуется указать последовательность действий, при которой осуществляется требуемое переливание и выполнены все условия задачи.
Если не сказано ничего другого, считается, что
- все сосуды без делений
- нельзя переливать жидкости "на глаз"
- невозможно ниоткуда добавлять жидкости и никуда сливать
Мы можем точно сказать, сколько жидкости в сосуде, только в следующих случаях.
1) знаем, что сосуд пуст,
2) знаем, что сосуд полон, а в задаче дана его вместимость,
3) в задаче дано, сколько жидкости в сосуде, а переливания с использованием этого сосуда не проводились
4) в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, и после переливания вся жидкость поместилась в один из них
5) в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, известна вместимость того сосуда, в который переливали, и известно, что вся жидкость в него не поместилась: мы можем найти, сколько ее осталось в другом сосуде
При решении задач используют следующие алгоритмы
Алгоритм I. - для решения задач первого типа.
1. Наполнить большую емкость жидкостью из бесконечного источника.
2. Перелить из большей емкости в меньшую емкость.
3. Вылить жидкость из меньшей емкости.
4. Повторить действия 1-3 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
Алгоритм II. - для решения задач второго типа
1. Из большей емкости наполнить емкость промежуточного объема.
2. Перелить жидкость из промежуточной емкости в самую маленькую емкость.
3. Перелить жидкость из самой маленькой емкости в большую емкость.
4. Повторять действия 2-3 до тех пор, пока емкость промежуточного объема не станет пустой.
| Задача №1. Как пользуясь банками в 3л и 5л, щенку Антошке набрать воды ровно 1л? | ||||||||||
| Сосуды | ПЕРЕЛИВАНИЯ | |||||||||
| 5 литров | - | 3 | 3 | 5 (3+2) | ||||||
| 3 литра | 3 | - | 3 | 1 | ||||||
|
| ||||||||||
| Сосуды | ПЕРЕЛИВАНИЯ | |||||||||
| 5 литров | 3 | 3 | 5 (3+2) | 1 | 1 | 4 (1+3) | ||||
| 3 литра | 3 | 3 | 1 (3-2) | 3 | ||||||
|
| ||||||||||
| Сосуды |
ПЕРЕЛИВАНИЯ | |||||||||
| 12 литров | 12 | 4 (12-8) | 4 | 9 (4+5) | 9 | 1 (9-1) | 1 | 6 (1+5) | ||
| 8 литров | 8 | 3 (8-3) | 3 | 8 | 6 (8-2) | 6 | ||||
| 5 литров | 5 | 3 | 3 | 5 (3+2) | ||||||
·
Курс подготовки к олимпиадам 5-6 класс
· Математические ребусы
· Задачи на четность и нечетность
· Восстановление математических действий
· Задачи на нахождении площади
· Задачи на взвешивание
· Задачи на переливание
· Задачи на рыцарей и лжецов
· Делимость целых чисел и остатки
· Задачи на смеси
·
Задачи на рыцарей и лжецов
Теория > Олимпиада
Задачи о рыцарях и лжецах — разновидность увлекательных математических задач, в которых фигурируют персонажи:
Лжец (плут, вампир, сумасшедший, оборотень) — человек, всегда говорящий ложь.
Рыцарь (человек, поступающие правдиво и правильно, правдец) - человек, говорящий всегда правду.
Решение подобных задач обычно сводится к перебору вариантов с исключением тех, которые приводят к противоречию.
Существуют задачи с тремя типами персонажей — рыцари, лжецы и нормальные люди (вариант - шпионы). Последние могут как лгать, так и говорить правду.
Задача №1 : По кругу сидят рыцари и лжецы – всего 12 человек. Каждый из них сделал заявление: «Все кроме, быть может, меня и моих соседей – лжецы". Сколько рыцарей сидит за столом, если известно, что лжецы всегда врут, а рыцари всегда говорят правду?
Решение:
Все не могут быть лжецами – тогда все заявления были бы истинными. Значит, есть рыцарь. Все, кроме, быть может, его двух соседей – лжецы. Оба соседа не могут быть лжецами – тогда они сказали бы правду; оба не могут быть рыцарями – тогда бы они солгали. Единственная оставшаяся возможность – один сосед — лжец, другой – рыцарь (то есть два рыцаря рядом, остальные — лжецы) удовлетворяет условиям задачи.
Ответ: 2 рыцаря.
Задача №2 : На острове живут 100 рыцарей и 100 лжецов, у каждого из них есть хотя бы один друг. Рыцари всегда говорят правду, а лжецы всегда лгут. Однажды утром каждый житель произнес фразу «Все мои друзья — рыцари», либо «Все мои друзья — лжецы», причем каждую из фраз произнесло ровно 100 человек. Найдите наименьшее возможное число пар друзей, один из которых рыцарь, а другой — лжец.
Решение: Заметим, что в паре рыцарь-лжец каждый должен сказать, что другой лжец: рыцарь скажет правду, а лжец соврёт, в паре рыцарь-рыцарь оба скажут правду, а в паре лжец-лжец оба скажут неправду. Значит фраза «Все мои друзья — лжецы» употребляется только в парах рыцарь-лжец. Минимальное кол-во пар рыцарь-лжец, когда фразу сказали 100 человек, это 50. Если пар будет меньше, то и фраз тоже будет меньше.
Задача №3 : Перед нами трое людей A, B и C. Один из них рыцарь, другой лжец и третий - нормальный человек Эти люди высказывают следующие утверждения.
A: Я нормальный человек.
B: Это правда.
C: Я не нормальный человек.
Кто такие A, B и C?
Решение: Прежде всего заметим, что A не может быть рыцарем, потому что рыцарь не назвал бы себя нормальным человеком. Следовательно получается что, A - либо лжец, либо нормальный человек. Тогда истинно высказывание человека B. Значит, B - либо рыцарь, либо нормальный человек. Но B не может быть нормальным человеком (так как A - нормальный человек), поэтому B - это доблестный рыцарь, а C - маленький лжец. Но лжец не может сказать о себе, что он не нормальный человек (так как любой лжец - не нормальный человек), и мы приходим к противоречию. Итак, A не может быть нормальным человеком. Следовательно, A - хитрый лжец. Это означает, что высказывание человека B ложно, в силу чего B должен быть нормальным человеком (лжецом он быть не может, так как лжец - человек A). Итак, A - хитрый лжец, а B - нормальный человек. Отсюда мы заключаем, что C - доблестный рыцарь.
Задача №4 : Двое людей A и B, о которых известно, что каждый из них либо рыцарь, либо лжец, либо нормальный человек, высказывают следующие утверждения:
A: B - рыцарь.
B: A - не рыцарь.
Докажите, что по крайней мере один из них говорит правду, но это не рыцарь.
Решение: Эта задача обладает интересной особенностью. Условия ее не позволяют установить, кто из двух островитян говорит правду, не будучи рыцарем: A или B. Мы можем доказать более слабое утверждение: по крайней мере один из двух островитян A и B говорит правду, не будучи рыцарем. Островитянин A либо говорит правду, либо не говорит правду. Докажем два утверждения: 1) если A говорит правду, то он говорит правду, не будучи рыцарем; 2) если A лжет, то B говорит правду, не будучи рыцарем.
1) Предположим, что A говорит правду. Тогда B - рыцарь и, следовательно, говорит правду. Значит, A - не рыцарь. Таким образом, если A говорит правду, то A - лицо, говорящее правду, не будучи рыцарем.
2) Предположим, что A не говорит правду. Тогда B - не рыцарь. Но B должен говорить правду, так как A не может быть рыцарем (ведь A не говорит правду). Следовательно, в этом случае B говорит правду, не будучи рыцарем.
Задача №5 : Трое людей A, B и C, о каждом из которых известно, что он либо рыцарь, либо лжец, либо нормальный человек, высказывают следующие утверждения: A:
B по рангу выше, чем C.
B: C по рангу выше, чем A.
Затем у C спрашивают: "Кто старше по рангу - A или B?" Что ответит C?
Решение: Первый шаг. Прежде всего докажем, что в силу высказывания A островитянин C не может быть нормальным человеком. Действительно, если A - рыцарь, то B - особа более высокого ранга, чем C. Следовательно, B должен быть нормальным человеком, а C - лжецом. Таким образом, в этом случае C - не нормальный человек. Предположим, что A - лжец. Тогда B по рангу не выше C. Следовательно, B - особа более низкого ранга, поэтому B должен быть нормальным человеком, а C - рыцарем. Таким образом, и в этом случае C - не нормальный человек. Предположим, наконец, что A - нормальный человек. Тогда C - заведомо не нормальный человек (так как из трех островитян A, B и C только один – нормальный человек). Итак, C - не нормальный человек.
Второй шаг. При аналогичных рассуждениях из высказывания B можно вывести, что A - не нормальный человек. Таким образом, ни A, ни C не нормальны. Следовательно, B - нормальный человек.
Третий шаг. Поскольку C - не нормальный человек, то он может быть рыцарем или лжецом. Предположим, что он рыцарь. Тогда A - лжец (так как B - нормальный человек). Следовательно, B - особа более высокого ранга, чем A, и C, будучи рыцарем, даст правдивый ответ: "В по рангу выше A". С другой стороны предположим, что C - лжец. Тогда A должен быть рыцарем, поэтому B по рангу не выше A. В этом случае C, будучи лжецом, солгал бы и ответил так: "В по рангу выше A". Таким образом, независимо от того, кто такой островитянин C - рыцарь или лжец, он ответит, что B по рангу выше A
·
Курс подготовки к олимпиадам 5-6 класс
· Математические ребусы
· Задачи на четность и нечетность
· Восстановление математических действий
· Задачи на нахождении площади
· Задачи на взвешивание
· Задачи на переливание
· Задачи на рыцарей и лжецов
· Делимость целых чисел и остатки
· Задачи на смеси
·
Дата добавления: 2018-11-24; просмотров: 477; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!