Спектральное представление случайных процессов.

Если 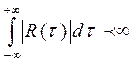, то можно вместо корреляционной функции использовать ее изображение – спектральную плотность.

Удобства спектральной плотности в том, что формулы описания преобразования случайных процессов упрощаются, и вместо интегрирования появляется операция умножения.

Спектральная плотность может быть введена и для нестационарных процессов, но наибольшую практическую значимость имеет описание стационарных процессов.

 Спектральная плотность это изображение оригинала:

;

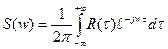обратное преобразование:

;

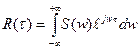Свойства спектральной плотности:

1. ;

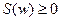2. 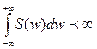- это условие для некоторых процессов (искусственно придуманных математиками например «белый шум» ), не подходит;

3. 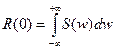- дисперсия;

4. 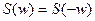- для действительных функций;

5. ;

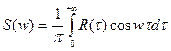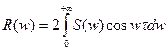 обычно спектральную плотность удваивают за счет симметричности для w>0;

6. Взаимно корреляционная функция имеет изображением взаимную спектральную плотность: 

;

.

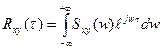Пример:

Задано:

;

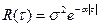Находим спектральную плотность:

;

   

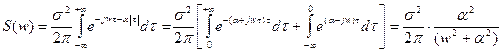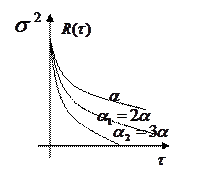
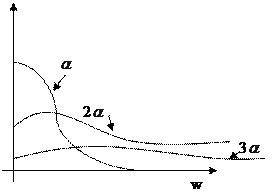
Белый шум.

С точки зрения физики таких процессов не бывает, но с точки зрения математики это удобно.

Белый шум имеет спектральную плотность: ;

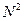- интенсивность белого шума

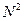- подчеркивает что число положительное

Белый шум – это процесс, у которого спектральная плотность не зависит от частоты,

дисперсия равна бесконечности, а корреляционная функция: если 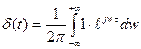, то

,

.

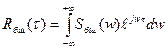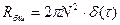Многие формулы(в разных книгах) верны с точностью до коэффициента 2 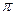 и 4 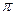² , для решений практических задач это обычно не имеет значения.

Белым шумом можно назвать процесс имеющий постоянную спектральную плотность и этот процесс действует на систему у которой полоса пропускания гораздо меньше полосы действия сигнала.То есть реальную S(w) 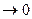,заменяем на S(w) 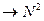(математическая абстракция)

 

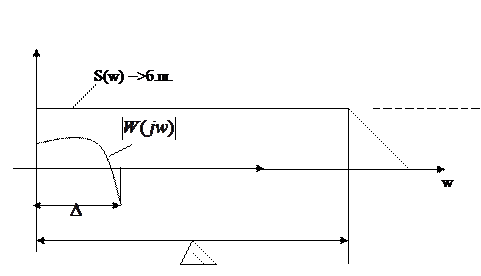
Связь между спектральными плотностями случайных сигналов в линейной системе с импульсно переходной функцией k( )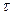

^;

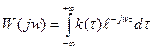 Мы рассматриваем здесь все для стационарных систем.

                                                 x(t)                  y(t)

 

Выходной сигнал: ;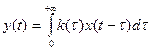

Математическое ожидание выходного сигнала: ;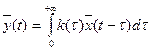

Вычитаем:

Обозначаем:

_;

;

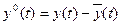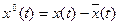тогда:

вычисляем математическое ожидания от обоих частей полученного выражения:

;

;

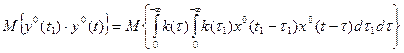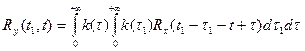Домножаем:

;

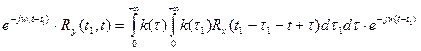вычисляем интеграл от обеих частей:

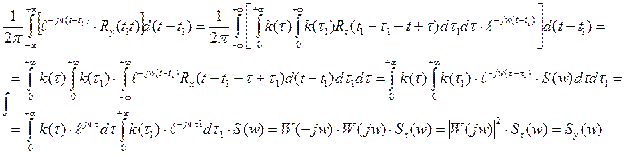Пример:

Есть система:

На вход системы действует «белый шум»:ξ(t). Найти характеристики процесса y(t) на выходе системы.

	y(t)

Корреляционная функция «белого шума»:

;

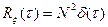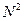- известное число

Спектральная плотность выходного сигнала: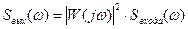

;

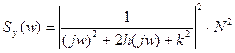Обозначения:

Имеем:

 ;

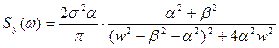или

;

 

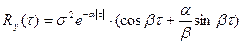Прохождение случайных процессов в линейной системе, оценка ошибок.

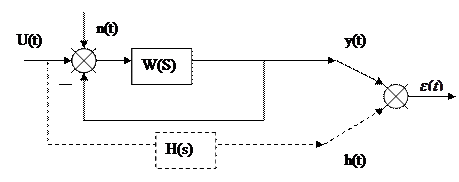
Структура системы задана. Передаточная функция разомкнутой системы: W(S) - известна

U(t) – Изменяемый(входной, полезный) сигнал. Желательно чтобы U(t) преобразовывалось системной с передаточной функцией: H(s). (Известна : S_u(ω))

Желательно чтобы n(t) преобразовывалась системой с передаточной функцией: 0.

n(t) – помеха.

h(t) – идеальный выходной сигнал.

y(t) – реальный выходной сигнал.

- ошибка(из-за помехи n(t) и искажения полезного сигнала u(t) реальной системой )

Запишем ошибку в области изображений(легче всего):

;

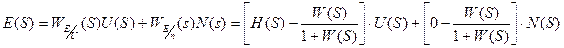Спектральная плотность ошибки (как выходного сигнала) тогда будет:

;

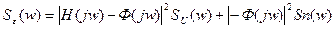где: 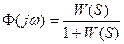 - передаточная функция замкнутой системы (от u(t) и n(t) до y(t))

здесь они одинаковы.

Тогда дисперсия ошибки в работе системы:

 

;

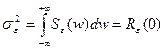Знание: 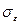 позволяет оценить диапазон, в котором будет находиться ошибка: 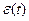(строго это для гауссовых процессов). Обычно(но не всегда):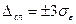

 

---

Дата добавления: 2018-11-24; просмотров: 193; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!