Скалярний, векторний та мішаний добутки векторів
Задача 2.10. Дано вектори  та
та  . Обчислити:
. Обчислити:
1) 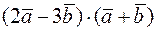 ;
;
2) 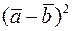 .
.
Розв’язання. 1) Знайдемо координати векторів співмножників.
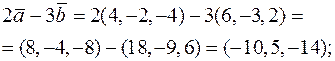
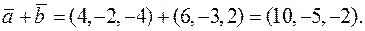
• Якщо  та
та 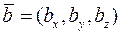 , то їх скалярний добуток знаходиться за формулою
, то їх скалярний добуток знаходиться за формулою
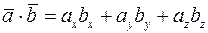 ,
,
тобто
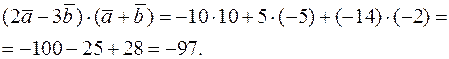
2) Знайдемо координати 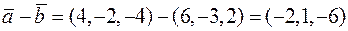 . Тоді
. Тоді 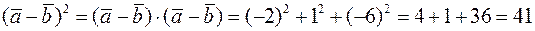 .
.
Задача 2.11. Дано вершини чотирикутника 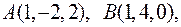
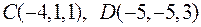 . Довести, що його діагоналі перпендикулярні.
. Довести, що його діагоналі перпендикулярні.
Розв’язання. На діагоналях чотирикутника розташовані вектори  та
та  .
.
• Два вектори перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.
Тому обчислимо
 ,
,
з чого й випливає перпендикулярність діагоналей чотирикутника.
Задача 2.12. Дано вершини трикутника АВС 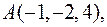
 та
та 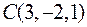 . Визначити його внутрішній кут при вершині В.
. Визначити його внутрішній кут при вершині В.
Розв’язання. Зобразимо трикутник:
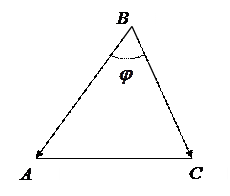
Кут при вершині В– це кут між векторами  та
та 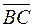 . Маємо
. Маємо 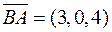 ,
, 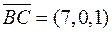 .
.
• Косинус кута між векторами 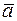 та
та  обчислюється за формулою
обчислюється за формулою
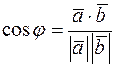 .
.
У нашому випадку  .
.
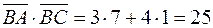 ,
,  .
.
Тоді 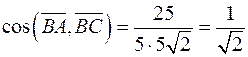 , значить, кут при вершині В дорівнює
, значить, кут при вершині В дорівнює  .
.
Задача 2.13. Дано 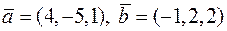 та
та 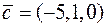 . Знайти
. Знайти  .
.
Розв’язання. Обчислимо суму векторів  .
.
• Скалярна проекція вектора 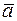 на вісь вектора
на вісь вектора  обчислюється за формулою
обчислюється за формулою
 .
.
В нашій задачі
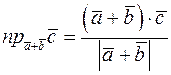 .
.
Далі знайдемо
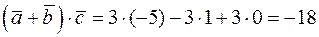 ,
,
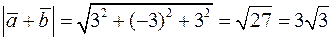 .
.
Тоді 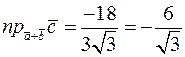
Задача 2.14. Дано вектори  та
та 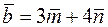 , де
, де 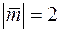 ,
, 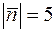 , кут між векторами
, кут між векторами  та
та  дорівнює
дорівнює 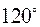 . Знайти:
. Знайти:
1) 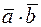 ;
;
2) 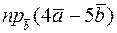 ;
;
3) косинус кута між векторами 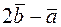 та
та 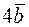 .
.
Розв’язання. Особливість цієї задачі полягає в тому, що координати векторів 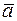 і
і  невідомі, тому не вдасться скористатись зручною формулою для обчислення скалярного добутку через координати. Для обчислення скалярного добутку в цій задачі ми будемо користуватись властивостями скалярного добутку та формулою
невідомі, тому не вдасться скористатись зручною формулою для обчислення скалярного добутку через координати. Для обчислення скалярного добутку в цій задачі ми будемо користуватись властивостями скалярного добутку та формулою
|
|
|
• 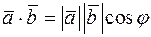 ,
,
де  – це кут між векторами
– це кут між векторами 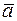 і
і  .
.
Зазначимо, що властивості скалярного добутку значною мірою схожі на властивості звичайної операції множення чисел, тому можна розкривати дужки, приводити подібні доданки, при необхідності переставляти множники місцями.
1) Обчислимо
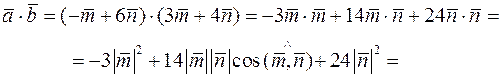
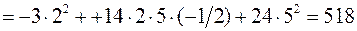 .
.
При обчисленні ми скористались тим, що
 .
.
2) Нехай 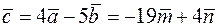 . Тоді
. Тоді  ,
,
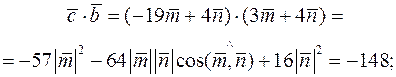
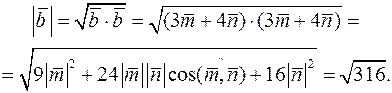
Остаточно маємо
 .
.
3) Нехай 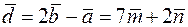 ,
,  . Тоді
. Тоді
 ,
,
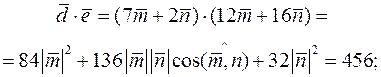

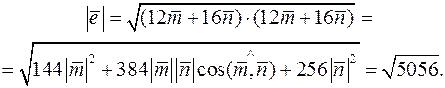
В результаті маємо:
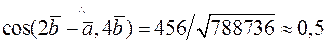 .
.
Задача 2.15. Дано 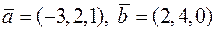 та
та  . Знайти векторний добуток
. Знайти векторний добуток 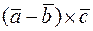 .
.
Розв’язання.
• Якщо координати векторів 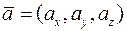 та
та 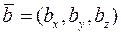 , то їх векторний добуток можна знайти за допомогою символічного визначника
, то їх векторний добуток можна знайти за допомогою символічного визначника
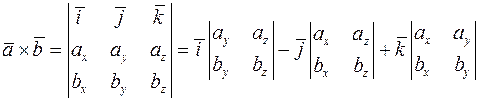 .
.
Спочатку знайдемо координати вектора
 .
.
Далі
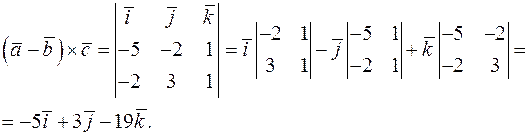
Задача 2.16. Знайти площу паралелограма, побудованого на векторах 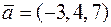 та
та 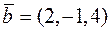 .
.
Розв’язання.
• Площа паралелограма, побудованого на векторах 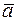 і
і 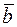 , знаходиться за формулою
, знаходиться за формулою 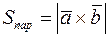 .
.
• Відразу зауважимо, що площа трикутника, побудованого на векторах 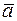 і
і 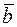 складає половину площі паралелограма, тобто
складає половину площі паралелограма, тобто
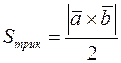 .
.
Обчислимо векторний добуток  :
:
|
|
|
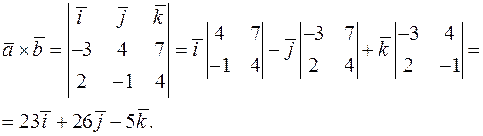 Відповідно
Відповідно  .
.
Задача 2.17. Знайти площу паралелограма, побудованого на векторах 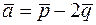 та
та 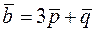 , якщо відомо, що
, якщо відомо, що 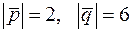 , та кут між векторами
, та кут між векторами  і
і 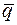 дорівнює
дорівнює 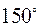 .
.
Розв’язання. Як і в задачі 2.14, особливість цієї задачі полягає в тому, що координати векторів 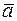 і
і 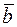 невідомі. Для обчислення векторного добутку в цій задачі, ми будемо скористаємось властивостями векторного добутку та формулою для знаходження модуля векторного добутку
невідомі. Для обчислення векторного добутку в цій задачі, ми будемо скористаємось властивостями векторного добутку та формулою для знаходження модуля векторного добутку
• 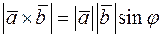 ,
,
де  – це кут між векторами
– це кут між векторами 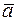 і
і 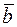 .
.
Зауважимо, що звичайним студентським заблудженням є впевненість в тому, що дана формула дозволяє знаходити векторний добуток. Але це зовсім не так. Векторний добуток – це вектор, для визначення якого потрібно задавати не лише його модуль, але й напрямок. Таке визначення легко знайти у підручнику. Записана формула дозволяє знайти лише модуль цього вектора.
Далі зазначимо, що властивості векторного добутку, як і скалярного, деякою мірою схожі на властивості звичайної операції множення чисел, тому можна розкривати дужки, приводити подібні доданки. Але при цьому слід брати до уваги, що є дві властивості, якими векторний добуток відрізняється від скалярного, чи ж то від звичайного множення чисел. По-перше,
|
|
|
• 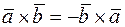 ,
,
по-друге, для будь-якого вектора
•  .
.
Тепер перейдемо до розв’язання нашої задачі.
Використовуючи властивості векторного добутку, виразимо векторний добуток 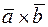 через векторний добуток векторів
через векторний добуток векторів 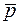 і
і 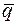 :
:
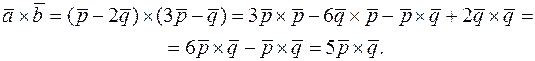
Далі обчислимо площу паралелограма
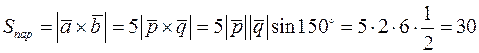 .
.
Задача 2.18. Дано 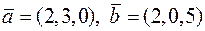 та
та 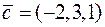 . Знайти мішаний добуток
. Знайти мішаний добуток 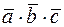 .
.
Розв’язання.
• Якщо координати векторів 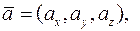
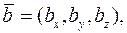
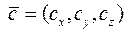 , то їх мішаний добуток можна знайти за формулою
, то їх мішаний добуток можна знайти за формулою
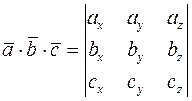 .
.
В нашій задачі одержимо
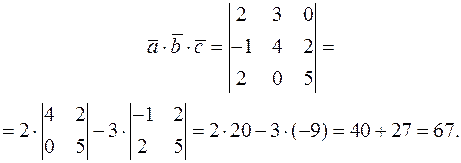
Задача 2.19. Довести, що чотири точки 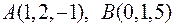 ,
, 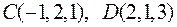 лежать в одній площині.
лежать в одній площині.
Розв’язання. Знайдемо координати трьох векторів 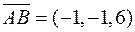 ,
,  ,
, 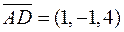 . Далі помітимо, що задані чотири точки розташовані в одній площині тоді, коли три знайдені вектори компланарні.
. Далі помітимо, що задані чотири точки розташовані в одній площині тоді, коли три знайдені вектори компланарні.
• Відомо, що три вектори компланарні тоді і лише тоді, коли їх мішаний добуток дорівнює нулю.
Знайдемо мішаний добуток
 .
.
Для обчислення визначника скористаємось його розкладанням за елементами другого рядка.
 .
.
Оскільки мішаний добуток дорівнює нулю, то вектори компланарні, отже чотири точки знаходяться у одній площині.
Задача 2.20. Знайти об’єм паралелепіпеда, побудованого на векторах 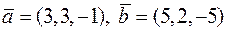 та
та 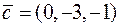 , що виходять з однієї точки.
, що виходять з однієї точки.
Розв’язання.
• Об’єм паралелепіпеда, побудованого на трьох векторах 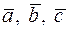 , що виходять з однієї точки, дорівнює модулю мішаного добутку цих векторів, тобто
, що виходять з однієї точки, дорівнює модулю мішаного добутку цих векторів, тобто
|
|
|
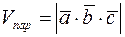 .
.
• Відразу зауважимо, що об’єм трикутної піраміди (тетраедра) побудованого на трьох векторах 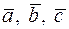 , що виходять з однієї точки складає шосту частину від об’єму паралелепіпеда, тобто
, що виходять з однієї точки складає шосту частину від об’єму паралелепіпеда, тобто
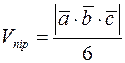 .
.
Обчислимо мішаний добуток
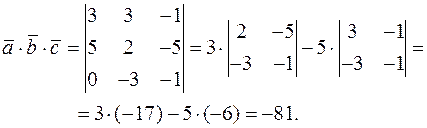
Тоді об’єм паралелепіпеда
 .
.
Задача 2.21. Вершини піраміди знаходяться в точках 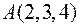 ,
,  ,
,  та
та 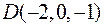 . Обчислити:
. Обчислити:
1) площу грані  ;
;
2) площу перерізу, який проходить через середину ребер 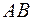 ,
, 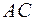 ,
, 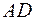 ;
;
3) об’єм піраміди  .
.
Розв’язання.
1) Грань піраміди представляє собою трикутник. Площа трикутника  дорівнює половині площі паралелограма, побудованого на векторах
дорівнює половині площі паралелограма, побудованого на векторах 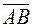 та
та 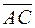 , тому
, тому 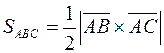 .
.
Маємо: 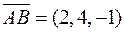 ,
,  . Значить
. Значить
 .
.
Остаточно одержимо: 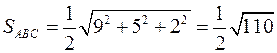 .
.
2) Використовуючи формулу для знаходження координат середини відрізка, знаходимо середини 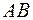 ,
, 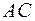 ,
, 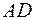 – точки
– точки 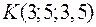 ,
,  ,
, 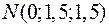 відповідно. Площу перерізу знайдемо за формулою
відповідно. Площу перерізу знайдемо за формулою
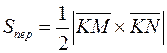 .
.
Координати векторів  ,
, 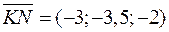 , тоді
, тоді
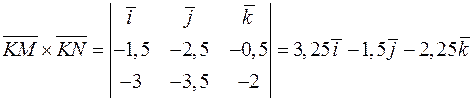 ,
,
 .
.
3) Оскільки
 ,
,
знайдемо координати векторів 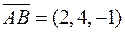 ,
,  ,
, 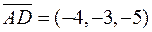 та їх мішаний добуток
та їх мішаний добуток
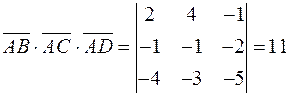 .
.
Отже, 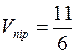 .
.
Задачі для самостійної роботи
1. Дано точки 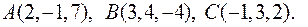 Обчислити
Обчислити 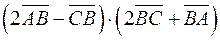 .
.
2. Обчислити площу паралелограма побудованого на векторах 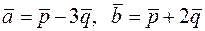 , якщо
, якщо 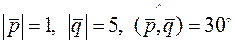 .
.
3. Вектори 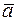 і
і 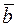 утворюють кут
утворюють кут 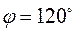 і
і 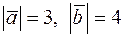 .Обчислити:
.Обчислити:  .
.
4. Дано вершини чотирикутника 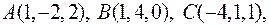
 . Перпендикулярні чи ні його діагоналі?
. Перпендикулярні чи ні його діагоналі?
5. Вектори 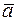 і
і 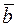 перпендикулярні і
перпендикулярні і 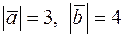 . Обчислити
. Обчислити 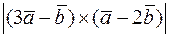 .
.
6. Довести, що чотирикутник з вершинами 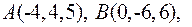
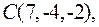
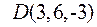 квадрат і обчислити його площу.
квадрат і обчислити його площу.
7. Обчислити об’єм піраміди  :
: 

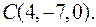
8. При якому значенні m вектори  перпендикулярні?
перпендикулярні?
9. Довести, що точки лежать у одній площині 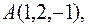
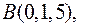
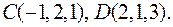
10. Знайти проекцію вектора 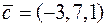 на вісь вектора
на вісь вектора 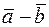 , де
, де 
 .
.
11. Знайти вектор, який перпендикулярний до векторів  та
та 
12. Знайти скалярний добуток векторів 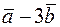
 та
та 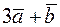 , де
, де 
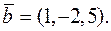
13. Обчислити площу трикутника 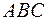 , якщо
, якщо 
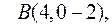

14. Перевірити компланарність векторів 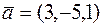 ,
, 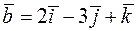 ,
, 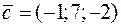 .
.
Дата добавления: 2018-11-24; просмотров: 435; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
