Ответ. 12 команд после включения в турнир новой команды.
В турнире с участием n команд проводится n(n-1)/2 игр (каждая из n команд сыграла n -1 игру, и при этом каждая игра получилась сосчитанной дважды). Поэтому условие можно записать так:
(n+1)n/2 = 1,2 n(n-1)/2, откуда 5n(n + 1) = 6 (n-1)n,
т.е. 5n + 5 = 6n – 6, n = 11.
Ответ. Не может.
Разность n ³ - n раскладывается в произведение (n - 1)n(n + 1) трех последовательных целых чисел, среди которых хотя бы одно число делится на 3. Поэтому эта разность делится на 3. Значит и разность кубов чисел и самих чисел должна делиться на 3, а она равна 700.
Ответы и решения 11 класс.
Ответ. 400.
Всего возможно 4 пары из первой и последней цифр таких, что первая цифра в два раза больше последней: 2 и 1, 4 и 2, 6 и 3, 8 и 4. А цифры, расположенные между ними, могут образовывать любое двузначное число (от 00 до 99), то есть каждая такая пара из первой и последней цифр дает 100 вариантов. Всего получается 4·100 = 400 вариантов.
2. Ответ: x = 2/7; y = 2/5, z = 2/3
Решение
Введем новые обозначения:
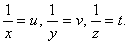 |
Получим:
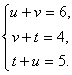 |
Складывая уравнения системы, получим 2(u +v+ t) = 15;
Теперь нетрудно получить u = 3,5; v = 2,5; t = 1,5,
тогда x = 2/7; y = 2/5, z = 2/3.
Ответ. Пятого велосипедиста.
Из условия следует, что первый велосипедист едет быстрее второго на 10 км/ч, третьего – на 20 км/ч, четвертого – на 30 км/ч, а пятого – на 40 км/ч. Это означает, что когда первый догонит второго, он в этот момент во второй раз догонит третьего, в третий раз – четвертого, в четвертый раз – пятого. Значит, в этот момент у него будет 1 + 2 + 3 + 4 = 10 обгонов. В момент, когда он во второй раз обгонит второго велосипедиста, у него получится 20 обгонов, и в этот момент все велосипедисты находятся рядом. Следующим будет обгон самого медленного – пятого велосипедиста.
|
|
|
4. Ответ. Все углы по 60º .
Пусть AD = x,CD =y , тогда, по условию, AB= 2y,CB =2x . По теореме Пифагора из треугольников ABD и CBD получаем: BD² = 4y² – x² = 4x² - y², откуда следует, что x= y . Тогда все стороны треугольника ABC равны 2x , значит, он – равносторонний.
Ответ. 11 партий.
Пусть первый сыграл со вторым A партий, первый с третьим – B партий, второй с третьим – C партий. Тогда. По условию, A+ B=21, A+ С=10.
Отсюда B – С = 11. Но тогда B ≥11, значит, A ≤ 21 - 11 =10 . Но A+ С=10, где C – неотрицательное число.
Значит, С=0, A=10, B=11. Поэтому третий сыграл B+ С=11 партий.
РЕКОМЕНДАЦИИ
ПО ПРОВЕДЕНИЮ ШКОЛЬНОГО ЭТАПА ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ШКОЛЬНИКОВ ПО МАТЕМАТИКЕ
ПОРЯДОК ПРОВЕДЕНИЯ ШКОЛЬНОГО ЭТАПА ПО МАТЕМАТИКЕ
Одной из важнейших задач Олимпиады на начальных этапах является развитие интереса у обучающихся к математике, создание мотивации к систематическим занятиям математикой на кружках и факультативах. Свойственные подростковому периоду стремление к состязательности, к достижению успеха, делают олимпиады привлекательными соревнованиями, где в честной и объективной борьбе обучающийся может раскрыть свой интеллектуальный потенциал. Кроме того, привлекательными являются условия нестандартных задач, предлагаемых на олимпиадах, заметно отличающиеся от обязательных при изучении школьного материала заданий, направленных на отработку выполнения стандартных алгоритмов (например, решения квадратных уравнений). Наконец, первые олимпиадные успехи важны для самооценки учащегося, а также изменения отношения к нему учителей, возможно недооценивавших его способности. Нередки случаи, когда способный и даже талантливый обучающийся не успевает за отведенное на уроке время выполнить все задания из контрольной работы по изучаемой теме. Необходимость решения сформулированных выше задач формирует подход к порядку проведения и характеру заданий на школьном этапе Олимпиады.
|
|
|
В олимпиаде имеет право принимать участие каждый обучающийся (далее –
Участник), в том числе вне зависимости от его успеваемости по предмету. Олимпиада должна проводиться в удобное для Участников время. Число мест в классах (кабинетах) должно обеспечивать самостоятельное выполнение заданий олимпиады каждым Участником. Продолжительность олимпиады должна учитывать возрастные особенности Участников, а также трудность предлагаемых заданий. Рекомендуемое время проведения олимпиады:
|
|
|
Дата добавления: 2018-11-24; просмотров: 107; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
