Напряжения и деформации с учетом собственного веса

 

Определим напряжения и деформации в призматическом стержне в учетом собственного веса. Стержень длиной l и площадью поперечного сечения F изготовлен из материала плотностью γ (рис. 3.7 а, в, с).

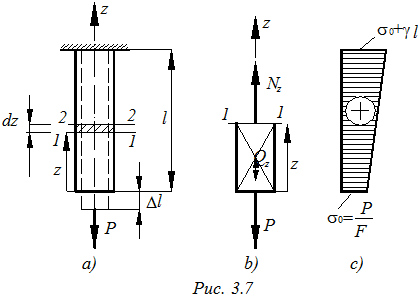На расстоянии z от точки приложения нагрузки проведем сечение 1:1 и рассмотрим в равновесии нижнюю часть стержня. Вес отсеченной части

Q_z = Vγ = Fzγ

V - объем материала.

Продольное усилие N_z найдем как:

ΣF_z = 0  N_z – Q_z – P = 0 или N_z = Q_z + P

Напряжение

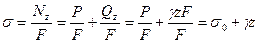                                                                               (3.8)

0£ z £l; z = 0, σ_z = 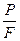= σ₀; z = l, σ_z = σ₀ + γl;

Эпюра напряжений показана на рис. 3.7 с.

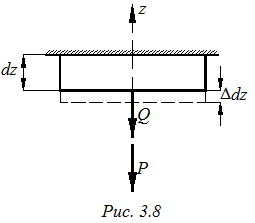Для определения Δl рассмотрим деформацию части стержня длиной dz (рис. 3.8).

Согласно формуле (3.7) можно записать

Δdz= ;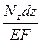

или

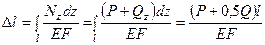               (3.9)

Здесь Q = Fγl.

 

Стержень равного сопротивления при растяжении и сжатии

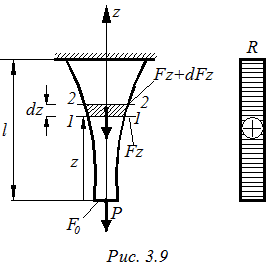
В призматических стержнях напряжения от собственного веса по высоте сечения распределены не равномерно (рис.3.7в). Следовательно, материал элемента используется не эффективно. Запроектируем такой стержень, у которого по всей длине в любом сечении напряжения одинаковы и равны заданной величине σ = R = const (рис. 3.9).

С этой целью установим закон изменения площади поперечного сечения по длине элемента. Площадь нижнего сечения может быть найдена из условия

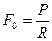
В сечении 1:1, взятом на расстоянии z от нижнего конца площадь равна F_z. В сечении 2:2, взятом на расстоянии dz oт предыдущего сечения, за счет приращения веса dQ_z, площадь сечения увеличится и станет равной F_z + dF_z. Cледовательно, чтобы напряжения во всех сечениях были одинаковы необходимо, чтобы приращение веса элемента к приращению площади сечения оставалось постоянной величиной.

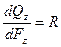               или   

Разделяя переменные, получим дифференциальное уравнение:

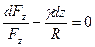
Решение этого уравнения:

ln F_z - 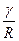z + C = 0

Здесь C - произвольная постоянная, которую можно найти из условия:

z =0 F_z = F₀, , следовательно,        ln F₀ + C = 0 отсюда ln F₀ = - C

ln F_z – z – ln F_z = 0

ln 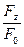 = 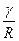z

Потенцируя это выражение, найдем:

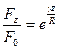или

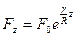                                                             (3.10)

Из формулы (3.10) следует, что площадь поперечного сечения по длине элемента изменяется по логарифмической кривой. Вспомните очертания Останкинской и Эйфелевой башен. Они очерчены по кривой, так как одной из преобладающих нагрузок для них является собственный вес конструкции.

Для обычных элементов строительных конструкций сечение по высоте меняется ступенчато (стены гражданских зданий) или боковая поверхность элемента делается наклонной (опоры мостов).

 

Напряжения в сечениях, наклонных к оси стержня

 

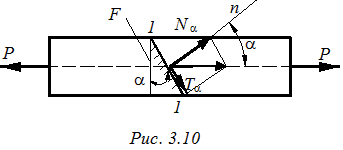В растянутом стержне проведем наклонное сечение 1:1, нормаль к которому n составляет угол α с продольной осью z (рис. 3.10).

F - площадь сечения элемента, нормального оси,

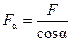 - площадь наклонного сечения элемента.

Из условия равновесия левой части имеем N = P.

Разложим N на две составляющие N_α и T_α:

N_α = Pcos α

T_α = Psin α

Полагая, что нормальные и касательные напряжения по наклонному сечению распределены равномерно, найдем:

                                    σ_α = 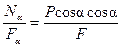 = σ₀cos² α                                            (3.11)

                                    τ_α = 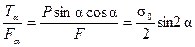                                                (3.12)

Из формулы (3.11) следует, что σ_max = σ_α, cos α = 1 при α = 0.

Касательные напряжения в этом случае τ_α = 0.

Наибольшие касательные напряжения возникают на площадке, наклоненной под углом α =±45⁰ к оси z; sin 2α = 1, 2α = 90⁰, α = 45⁰.

 τ_max =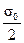

Нормальные напряжения на этих площадках равны касательным

σ_α=45 = = τ_max

Важно отметить, что нормальные и касательные напряжения на площадках, параллельных оси z, отсутствуют:

σ₉₀ = τ₉₀ = 0.

 

---

Дата добавления: 2018-11-24; просмотров: 380; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!