ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РЕШЕНИЕ УРАВНЕНИЙ

Методы вычисления определенных интегралов

Приближённое вычисление определенного интеграла основано на геометрическом смысле интеграла и сводится к приближенному вычислению площади, ограниченной графиком подынтегральной функции f(x), прямыми x = a = x₀, x = b = x_n и осью OX (рис. 19.1).

Рис. 19.1. График подынтегральной функции

Интервал [a, b] делится на n равных частей длиной .

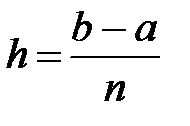Тогда значениям x_i = x_i-1 + h, i = 1,2, ..., n соответствуют значения y_i = f(x_i).

Метод прямоугольников. Согласно  методу левых прямоугольников, искомая площадь вычисляется как сумма площадей прямоугольников, основание которых равно h, а высота равна соответственно y₀ для первого прямоугольника, y₁ – для второго и т.д. вплоть до последнего с высотой y_n-1. Тогда

        

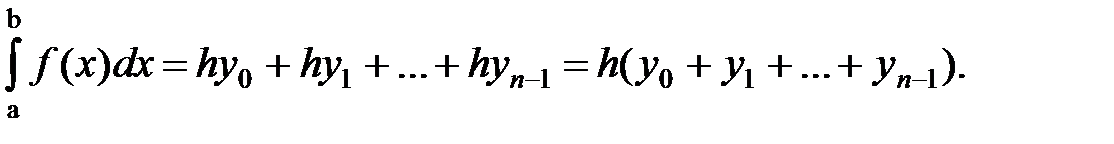
Для метода правых прямоугольников аналогично

Метод трапеций. По методу трапеций определяется сумма площадей трапеций, основаниями которых являются ординаты y₀, y₁ и т. д., а высоты равны h:

 

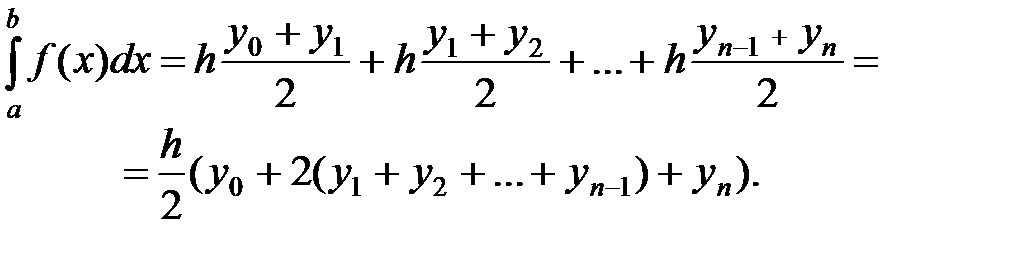
Погрешность метода оценивается как 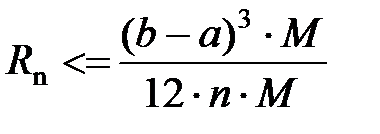, где М – максимальное значение второй производной f ( x ) на отрезке [ a , b ].Используя это соотношение, можно определить количество точек, на которое делится отрезок, исходя из заданной погрешности.

Значение интеграла, вычисленное по формуле трапеций, равно среднему арифметическому от значений интеграла, вычисленных по формулам левых и правых прямоугольников при том же разбиении.

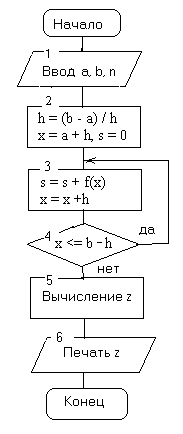
Рассмотрим алгоритм метода трапеций(рис. 19.2):

1. Ввод a, b, n.

2. Вычисление 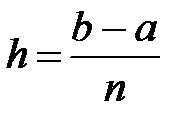, x = a + h,

s = 0.

3. Расчет s = s + f(x), x = x + h.

4. Если x > (b – h), то переход к пункту 5, иначе – переход к п. 3.

5. Вычисление значения интеграла

   

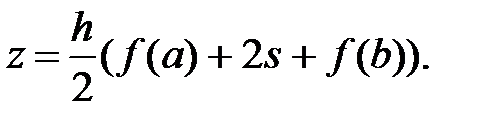
6. Вывод z.

Рис. 8.2. Схема алгоритма метода трапеций   2. Содержание задания 1. С помощью микрокалькулятора вычислить приближенно значение определенного интеграла из табл.1 для n =4. Номер варианта определяет преподаватель. Для нечетных по номеру вариантов использовать метод трапеций, для четных – метод парабол. 2. Написать программу, реализующую вычисление определённого интеграла соответствующим методом. Для всех вариантов принять n =20. 3. Выполнить вычисления в пакете MathCAD. Результаты сравнить между собой. Таблица 1 Номер вар. Функция Пределы интегри-рования Номер вар. Функция Пределы интегри-рования 1 x3+x-3 a=1, b=2 9 x3+3x-1 a=4, b=8 2 ln(x)+x+3 a=3, b=4 10 x3+x-1 a=3, b=4 3 x3+2x-11 a=6, b=7 11 ln(x)+x3 a=3, b=7 4 2ln(x)-1/x a=8, b=9 12 ex-2x2-1 a=2, b=9 5 2-x2+x a=1, b=3 13 2x+ln(x)+7 a=2, b=4 6 5x-1+x3 a=2, b=5 14 x3+2x-4 a=1, b=5 7 1+ex+x a=3, b=8 15 2-x+ln(x) a=3, b=7 8 x3+x-2 a=6, b=9 16 x2+4x+2 a =6, b =8   ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ апеций

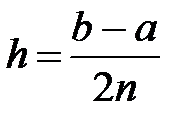Метод парабол (Симпсона). Согласно методу парабол интервал [ a , b ] делится на четное количество частей – 2 n. Тогда , x_i = x_{i –1} + h,

i = 1, 2, 3 …, 2n,

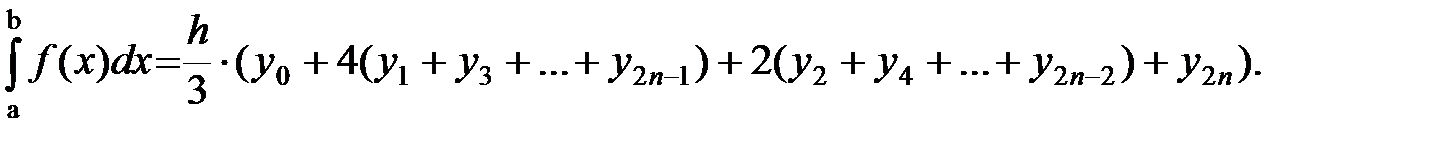
Алгоритм метода парабол:

1.  Ввод a, b, n.

2.  Вычисление 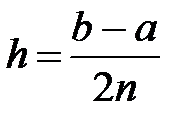, x = a + 2h, s1=0, s2=0, i=1.

3.  Расчет s2 = s2 + f(x) , x = x + h, s1 = s1 + f(x), x = x + h, i = i + 1.

4.  Если i < n – 1, то переход к п. 3, иначе – переход к следующему пункту.

5.  Вычисление значения интеграла:

  

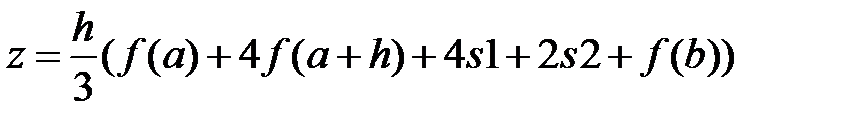
6.  Вывод z.

Здесь s1 = y₃ + y₅ + … + y_2n-1, а s2 = y₂ + y₄ + … + y_2n-2.

---

Дата добавления: 2018-11-24; просмотров: 181; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!